机器守门员 速度估计与落点预测
速度估计与落点预测分为以下三个部分， 分别是状态观测器、落点预测、以及扑救角度计算。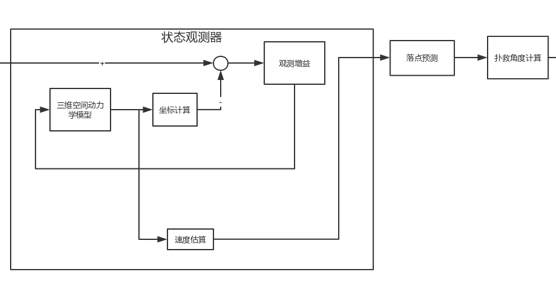最终达到的效果如下动图所示：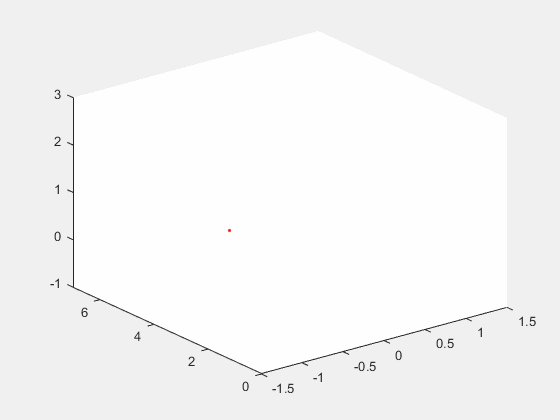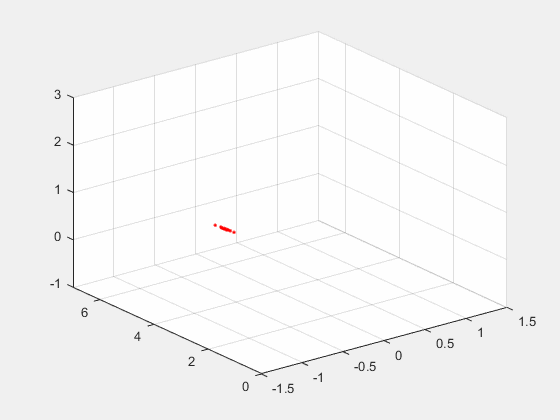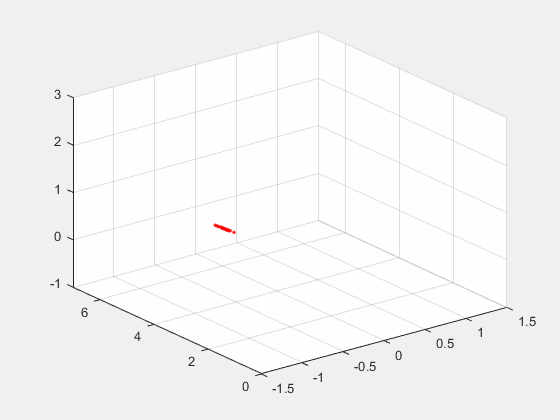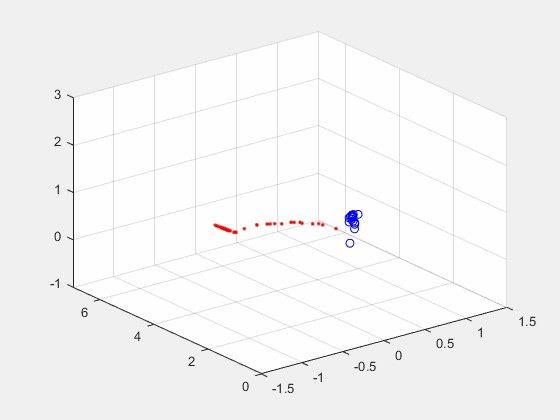
上图中红色的点为感知到的球的位置， 右边的坐标轴为x轴， 垂直的轴为y轴， xy轴构成的平面为球门所在平面。 初始时， 球静止放在大约7m的位置上， 由于深度的噪声可以看到静止状态下的坐标有些许噪声。 大约几秒钟后， 球被踢出， 红色的点记录了球在空间中的运动轨迹。 在球击出大概0.15s后， 球门平面上打出了蓝色的圈圈。 这个圈圈就是预测的破门点。
这就是状态估计与预测的作用， 输入为三维坐标点， 输出为破门点的坐标。 本章分三个内容来进行详细阐述：
[*] 状态观测器的设计：状态观测器是什么， 为什么需要状态观测器来估计速度？ 怎么设计这个状态观测器？
[*] 落点预测的方法：怎么通过速度来预测落点？
[*] 扑救角度的计算： 如何将落点换算为扑救角度？
一、 状态估计
本章内容对于从未接触过自动控制理论或是信息融合、机器人定位相关话题的读者有些不友好， 可以酌情跳过， 无需太过纠结。 状态估计的很多方法已经有成熟的库， 不了解其原理并不影响对其的使用。
1. 状态估计的需求来源
说起状态估计四个字， 对于普通读者来讲真是有些不友好。所谓状态估计这个词， 实际上建立在一套严密的系统状态表示方法上， 这是一套用于描述多维微分方程的描述体系， 在控制里面叫做”状态空间（state space）“， 但实际上我们可以用一个比较简单的例子来描述他。
比如说，问题1：现在有一辆车， 运动在一条笔直的线上， 假如说车辆做的是直线运动（加速减速不定）。 我们想要测量车当前的速度， 但是我们目前只能测量车相对道路标志的位移， 请问怎么做才能获得速度？
这个问题很好解决， 有高中物理的知识基本上就能回答：
每隔一段时间dt测量一次位移st, 测量两组数据后就能够得到速度， 计算(st+1 - st)/dt就能够精确的计算出车速了。如果用高等数学的思路来解释， 实际上就是直接对测量位移进行微分即可得到实时的车速。
问题2： 那么把这个问题再增加一点难度， 假如现在我们测量的位移是带有一定噪声的， 怎么办？
此时如果用同样的方法计算， 得出的速度就会包含比测量位移更大的噪声。 这该如何是好？
假如采样多次， 然后取平均值， 那么就丢失了在采样过程中变化的速度信息（在过程中加速了或者减速了怎么办）， 即丢失了高频信号。
这个问题就是一个典型的状态估计问题， 由于不能直接测量某物理量， 而需要微分或其他计算对其进行计算的情况下， 测量的误差或噪声就变成了一个巨大的问题。 而状态估计从另一个角度来解决这个问题。而车速的估计这个问题， 也是自动驾驶或者机器人定位中非常常见的一个状态估计问题， 常常用来解释卡尔曼滤波的工作原理与应用。
实际上， 状态估计的思路的核心在于预测+反馈修正。 首先， 用上一次估计的速度去预测现在时刻的位移， 然后用预测得到的位移和测量出来的带误差的位移进行减运算， 得到的差就经过反馈运算叠加到估计的状态上。 由于是反馈， 反馈环路是否收敛也需要被证明， 观测器的设计中已经包含了如何选取反馈增益来保证观测器收敛的方法。
2. 状态估计的常用方法
状态估计的常用方法比较多， 最出名的就是卡尔曼滤波算法， 名震四海， 工程实用性也很高。 其次就是状态观测器了， 状态观测器和卡尔曼滤波的区别在于没有增益自调节的环节， 也并没有将测量方差单独量化作为参数， 设计出发点也并没有从概率论角度进行考虑。 但在大部分观测方差变化不大的系统中， 观测器和卡尔曼滤波的效果差异也就不大了。
但是不管用什么方法， 状态估计的核心还是在于“误差收敛”， 也就是说要系统的输出介于预测和观测之间。 区别于直接计算的方法（如直接差分、微分）， 状态估计的核心在于有预测， 并且将预测的量和观测的量做出一种“融合”。
3. 状态观测器的好处
状态观测器相比较卡尔曼滤波而言， 参数较少， 可计算， 因此参数容易调教， 且参数意义较直观， 设计上比较简单， 对于观测噪声方差变化不大的简单系统非常适用。
而卡尔曼滤波虽然也能达到同样的效果， 但参数较观测器略多一些。 既然效果相似， 那么就用最简单的方法即可。
4. 状态观测器的设计
以上三个段落讲了太多抽象的内容， 反而容易造成误解和疑惑， 下面针对足球运动这个系统， 设计一个观测器， 来看看何为“预测”， 何为“观测”。
所谓预测， 就是根据上一时间点的所有状态， 估计下一时刻的所有状态。 什么东西能够描述足球提出后的运动， 从而能够根据上一时刻预测下一时刻呢？ 答案是： 微分方程组。
先来分析一下， x y z三个方向上的各自运动情况， 并且做出一些假设：
[*]x y z三个方向的运动是独立的
[*]以守门员的视角看， x方向为左右横向， y方向为上下垂向， z方向为前后纵向。
[*]左右横向的运动上， 忽略空气阻力， 球不受力。
[*]前后纵向的运动， 忽略空气阻力， 球不受力。
[*]垂向上， 球受重力， 向地面加速。
有了以上几点， 一个理想的抛物运动模型就能够建立了：
1. x方向上：x方向上位移的微分是x方向上的速度， x方向上的速度的微分是x方向的加速度， 在空中球不受横向的力， 因此加速度为0。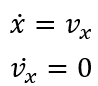
2. y方向上: y方向上位移的微分是y方向上的速度， y方向上的速度的微分是y方向的加速度， 在空中球受垂向地面的重力加速度， 因此加速度为-g。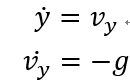
3. z方向上： z方向上位移的微分是x方向上的速度， z方向上的速度的微分是z方向的加速度， 在空中球不受纵的力， 因此加速度为0。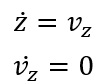
将几个式子联立：
设：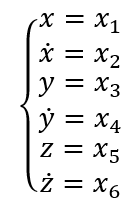
有：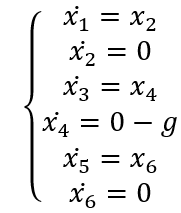
将上式写为矩阵形式：
简写为：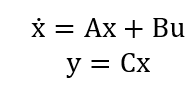
其中u为9.8.
以上就是球在三维空间内被踢出后的简化模型的状态空间形式。 利用该式， 已知某时刻的所有状态， 可以推测下一时刻的状态。 我们来测试一下是不是这样：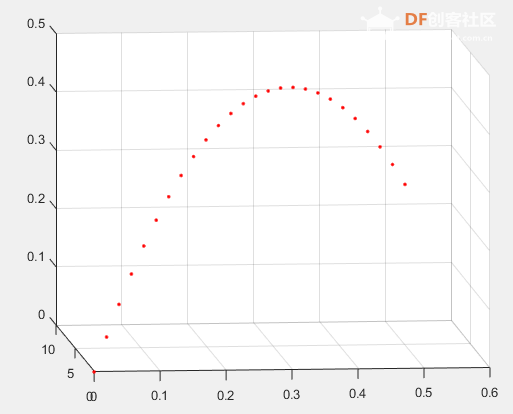
使用matlab进行一下仿真， 脚本如下：
A = ;
B = ;
C = ;
D = ;
y = lsim(sys,, , )
plot3(y(:,1),y(:,3),y(:,2),'r.')
从图上可以看出， 模拟球以速度从位置踢出， 球划过一个抛物线， 经过验算， 基本上符合物理事实。 这个模型将作为接下来用于预测的基础。
有了预测部分， 下面就是设计反馈部分了：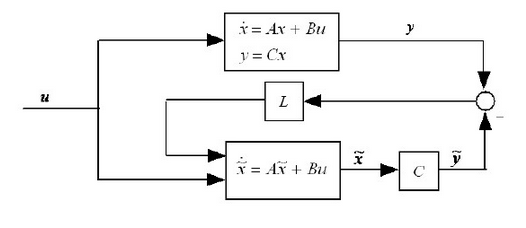
将估计的状态写为计算式：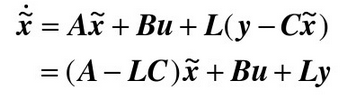
这个式子中L是我们要调节的观测器增益， L究竟取多大， 则是需要计算的。 如何计算呢？ 首先要分析L的物理含义：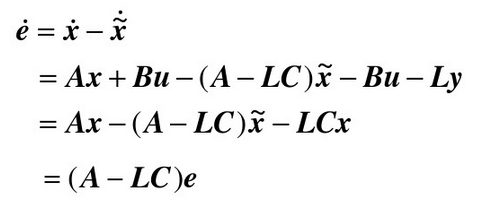
在这个误差分析中， 估计的状态与真实值得误差是一个动态关系， 而A-LC的特征根会决定误差的收敛速度。 理论上， L越大， 收敛速度越快， 反之收敛越慢。 但是不是L越大越好呢？ 也不是， 在噪声存在的情况下， L过大也会造成不收敛的情况。
根据需求， 我希望该观测器误差能在100ms内收敛到较低水平， 那么A-LC的特征根可以设计在[-10， -9 ， -10， -9， -10， -9]， 相对应L的值就取为：
L =
19.0000 90.0000 -0.0000 -0.0000 0.0000 0.0000
0.0000 0.0000 19.0000 90.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 19.0000 90.0000
此时， 预测、反馈观测都已经具备， 状态观测器的设计完毕， 接下来只需编码实现即可。
dX = A*X + L'*(measurement - Y);
X = X + dt*dX;
Y = C*X;
其中measurement就是上一章传感器测量到的三维坐标。 一组实测数据使用观测器效果如下：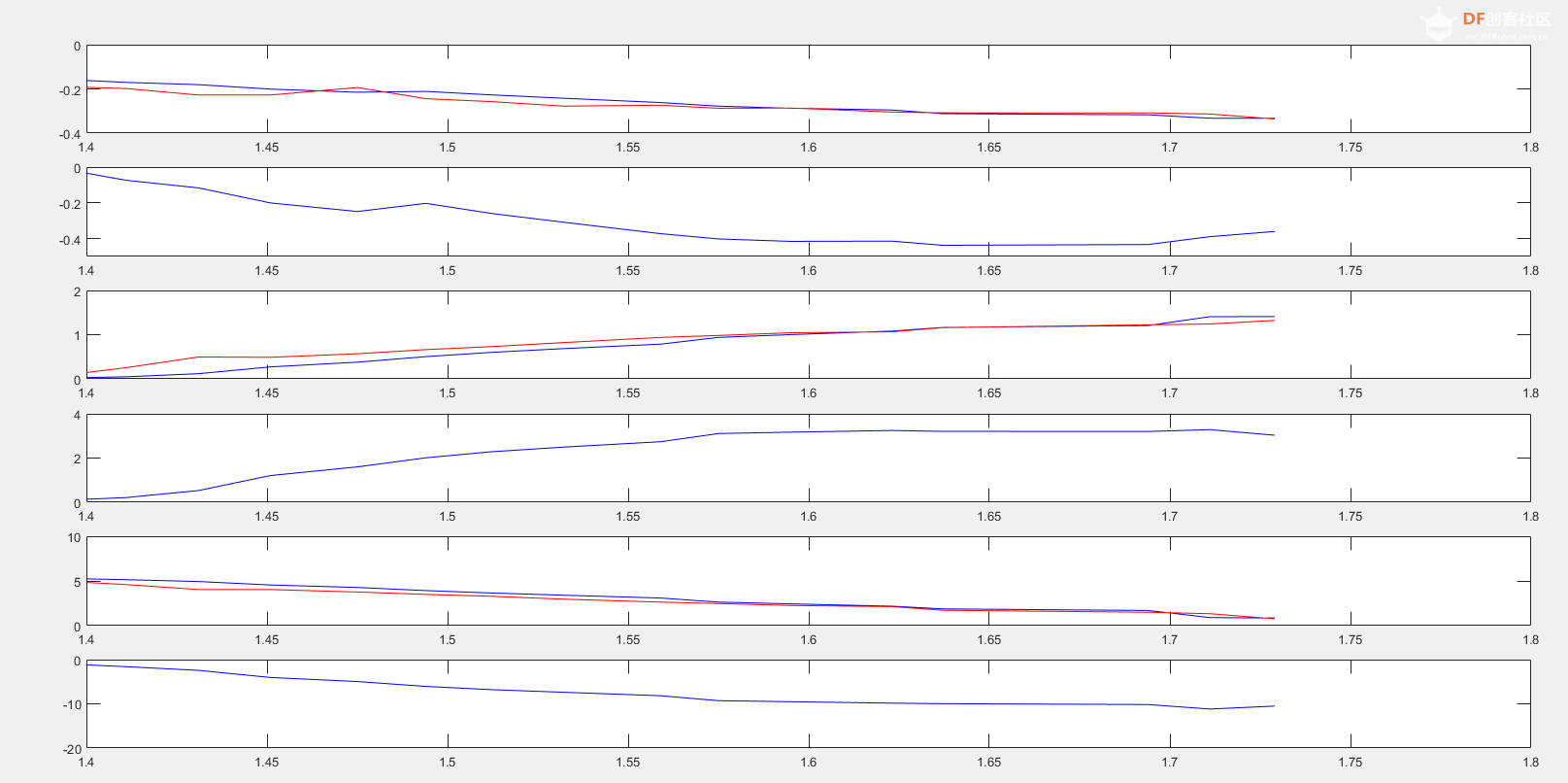
从上到下分别就是x1到x6， 可见， 速度值大概在0.15s左右收敛到比较接近真实的数值。 至此， 观测器设计基本完成了。
二、 落点估计破门点的估计上， 相对比较简单。
´利用空间几何计算， 速度向量与球门所在平面的交点， 并估算相交时间
´并根据自由落体公式和相交时间， 计算重力造成的下落距离， 以此预测球和球门平面的相交位置。
matlab代码如下：
function [ result ] = get_meetpoint( planevec, planepoint, linevec, linepoint )
vp1 = planevec(1);
vp2 = planevec(2);
vp3 = planevec(3);
n1 = planepoint(1);
n2 = planepoint(2);
n3 = planepoint(3);
v1 = linevec(1);
v2 = linevec(2);
v3 = linevec(3);
m1 = linepoint(1);
m2 = linepoint(2);
m3 = linepoint(3);
vpt = v1 * vp1 + v2 * vp2 + v3 * vp3;
if(vpt == 0)
result = [];
else
t = ((n1 - m1) * vp1 + (n2 - m2) * vp2 + (n3 - m3) * vp3) / vpt;
result = ;
end
end
函数输出的前三项为破门点的三维坐标， 第四项为飞行时间。
´根据预测的破门位置， 使用反三角函数(arctan)计算扑救的角度， 输出给到电机控制模块， 开始扑救动作。
学习了 跪着看完 不错不错 确实牛X！ 好深奥的赞赞赞 干懵了{:6_215:} 机器守门员的代码出售吗？厂长大哥
页:
[1]