高精度计算
# 为什么需要高精度计算对于 C++ 而言，最大的数据为 long long（64b，8位），对于超过 8B 的数据，C++ 没有对应的数据类型进行表示。所以我们需要知道高精度计算。更详细的解释，可以参考这个网页https://blog.csdn.net/justidle/article/details/104414459。
# 高精度加法计算原理
在读小学时，我们做加法都采用竖式方法，如图 1 所示。 这样，我们方便写出两个整数相加的算法。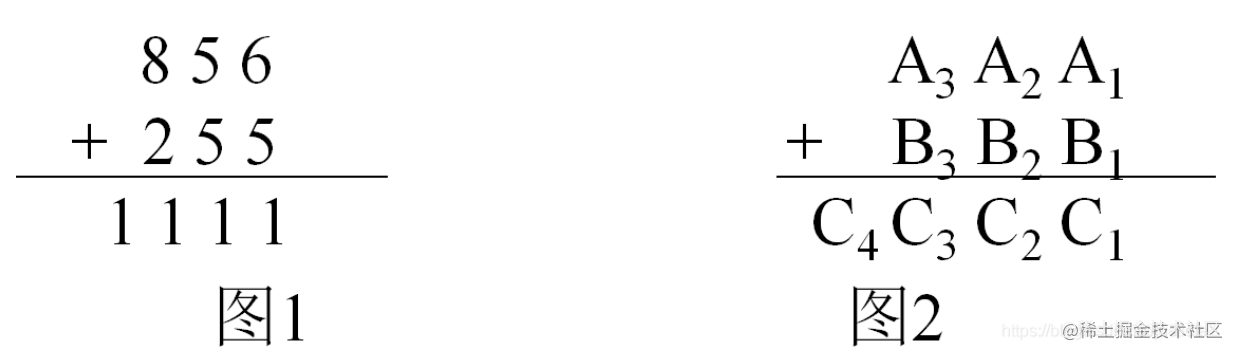
!(https://p6-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/e10eb69c162c467c8ec02c0707b4980d~tplv-k3u1fbpfcp-watermark.image?)
我们就可以用 C++ 语言来模拟这个竖式加法的过程。我们可以考虑利用 C++ 的数组来存储对应数据，假设用数组 A 存储 856 的每一位，具体来说就是 A1 存储个位 6，A2 存储十位 5，A3存储百位 8；类似数组 A 的结构，使用数组 B 存储 255；类似数组 A 的结构，使用数组 C 来存储对应的和 1111。两数相加的结果就如图 2 所示。这样理论上来说，我们就可以计算无限大的数据。如上图 2 所示，下表表示对应的存储方式。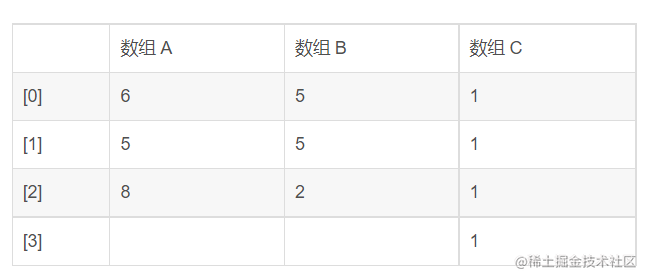
!(https://p1-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/4f35d0e19d2a4626a5d23f4c2b5a03e9~tplv-k3u1fbpfcp-watermark.image?)
总结：利用数组存储，突破存储的限制。每个位置存储 0 ~ 9 之间的数据。
# 高精度加法实现
## 思路
1、定义存储数组。
2、读入数据到数组中。注意是倒序存放，也就是个位放在数组下标为 0 的地方。
3、从个位开始模拟竖式加法的过程，完成整个加法。
4、删除前导 0 。所谓前导零，就是出现类似这样数据 01234，这个 0 实际是不需要的。
5、输出加法的结果。倒序输出加法的结果数组 C，因为我们的个位是存储在下标为 0 的地方。
## 技术细节说明
### 定义存储数组
根据题目的要求定义数组。这个部分代码如下：
```
const int MAXN = 1e5+4; //根据题目的最大值。+4为了防止A+B出现进位
char s1 = {};//存储字符串
char s2 = {};//存储字符串
int a = {};//存储加数A
int b = {};//存储加数B
int c = {};//存储和B
```
### 读入数据到数组
利用读入字符串的方法读入数据，再倒序写入到对应的数组中。这个部分代码如下：
```
scanf("%s %s", s1, s2);//读入字符串A
//将字符串写入到数组A中
int len1 = strlen(s1);
for (int i=0; i<len1; i++) {
//倒序写入
a = s1 - '0';
}
//将字符串写入到数组A中
int len2 = strlen(s2);
for (int i=0; i<len2; i++) {
//倒序写入
b = s2 - '0';
}
```
注意：我们需要保存加数 A 和加数 B 的最大长度。因为竖式加法需要。
### 模拟竖式加法
有两个技术细节：1、进位如何保存；2、最高位进位如何解决。这个部分代码如下：
//模拟竖式加法
int jw=0;//进位
int len = max(len1, len2)+1;//注意因为最高位可能出现进位
for (int i=0; i<len; i++) {
c = a + b + jw;//当前加数A位数据+加数B位位数据+上一位的进位
jw = c / 10;//本次加法是否存在进位
c %= 10;//只能保存 0 ~ 9 的数据
}
### 删除前导零
因为加法运算可能会出现最高位进位，所以我们在模拟竖式加法的时候多加了一位，所以我们需要判断是否需要删除前导零。这个部分代码如下：
//删除前导零
for (int i=len-1; i>=0; i--) {
//因为我们是从索引 0 开始，所以最高位是保存在 len-1
if (0==c && len>1) {
//注意要有 len>1 这个条件。考虑特殊情况，加法结果为 00，我们实际要输出 0。
len--;
} else {
//第一个不是零的最高位，结束删除
break;
}
}
### 输出计算结果
采用倒序的方式输出，因为我们数据保存是倒序结构，也就是低位在前。
//逆序打印输出
for (int i=len-1; i>=0; i--) {
printf("%d", c);
}
printf("\n");
## 例题和 AC 代码
### 题目
题目链接
一本通 OJ：http://ybt.ssoier.cn:8088/problem_show.php?pid=1168。
我自己 OJ：http://47.110.135.197/problem.php?id=1215。
### 题目描述
求两个不超过 200 位的非负整数的和。
### 输入
有两行，每行是一个不超过200位的非负整数，可能有多余的前导0。
### 输出
一行，即相加后的结果。结果里不能有多余的前导0，即如果结果是342，那么就不能输出为0342。
### 样例输入
22222222222222222222
33333333333333333333
### 样例输出
55555555555555555555
### 分析
题目告诉我们不超过 200 位，也就是 MAXN = 200+4。
## AC 代码
```
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 200+4; //根据题目的最大值。+4为了防止A+B出现进位
char s1 = {};//存储字符串
char s2 = {};//存储字符串
int a = {};//存储加数A
int b = {};//存储加数B
int c = {};//存储和B
int main() {
scanf("%s %s", s1, s2);//读入字符串A
//将字符串写入到数组A中
int len1 = strlen(s1);
for (int i=0; i<len1; i++) {
//倒序写入
a = s1 - '0';
}
//将字符串写入到数组A中
int len2 = strlen(s2);
for (int i=0; i<len2; i++) {
//倒序写入
b = s2 - '0';
}
//模拟竖式加法
int jw=0;//进位
int len = max(len1, len2)+1;//注意因为最高位可能出现进位
for (int i=0; i<len; i++) {
c = a + b + jw;//当前加数A位数据+加数B位位数据+上一位的进位
jw = c / 10;//本次加法是否存在进位
c %= 10;//只能保存 0 ~ 9 的数据
}
//删除前导零
for (int i=len-1; i>=0; i--) {
//因为我们是从索引 0 开始，所以最高位是保存在 len-1
if (0==c && len>1) {
//注意要有 len>1 这个条件。考虑特殊情况，加法结果为 00，我们实际要输出 0。
len--;
} else {
//第一个不是零的最高位，结束删除
break;
}
}
//逆序打印输出
for (int i=len-1; i>=0; i--) {
printf("%d", c);
}
printf("\n");
return 0;
}
```
版权声明：本文为CSDN博主「努力的老周」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/justidle/article/details/104424134
页:
[1]