四轴飞行器飞控研究（三）--姿态完整改进算法
继之前研究了一些飞行姿态理论方面的问题后，又找到了之前很流行的一段外国大神写的代码，来分析分析。第二篇文章的最后，讲到了文章中的算法在实际使用中有重大缺陷。
大家都知道，分析算法理论的时候很多情况下我们没有考虑太多外界干扰的情况，原因是很多情况下，传感器的精度以及受到的干扰并不会特别大，而显著的影响到算法。但是在IMU系统中，有点不同。由于地磁场十分微弱，而我们生活中有大量使用电子设备，使得磁场非常的混乱，以至于地磁传感器非常容易受到干扰。
由于以上算法把地磁传感器一同加入到姿态的测定中，并基本给予了地磁传感器与加速度传感器同样的加权，导致地磁传感器一旦被干扰，会对姿态产生地球重力突然被干扰一样的结果。。。对姿态的测量是毁灭性的。
综上，考虑到磁场的不稳定性，必须对地磁传感器进行降权处理，使得他对姿态的影响变小。
于是设计了以下的算法。
将磁场传感器的数据在姿态角度中剔除，更新姿态的俯仰角（PITCH）以及横滚角（ROLL）的时候只使用加速度传感器以及陀螺仪(角速度传感器)。
只在计算偏航角的（YAW）的时候使用磁场传感器。也就是只使用磁场传感器作为一个电子指南针，定位整个姿态在水平面旋转的角度。这样设计，让磁场传感器只影响姿态中的一个数值，减少了磁场的权重，即使磁场收到干扰，也不会导致姿态骤变，使得四轴坠机。 在对YAW进行计算的时候使用了如下函数。
eulerAngleRaw.yaw = 0.9 * (eulerAngleRaw.yaw - gzF*2*halfT) + 0.1 * angleMagYaw; 此处的0.9和0.1是可以变动的但他们相加应该为1，此处为一个最简单的1阶低通滤波器，增加0.1则是增大截止频率。
算法的流程图是这样的：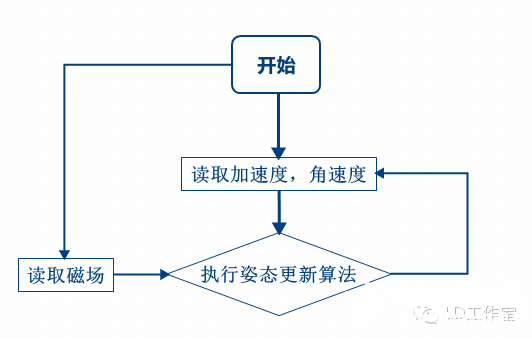
新的姿态更新算法是这样的void AHRSupdate(float gxf, float gyf, float gzf, float axf, float ayf, float azf, float mxf, float myf, float mzf)
{
double norm;
float vx, vy, vz;
float ex, ey, ez;
float halfT; //采样周期的一半
// 辅助变量，以减少重复操作数
float q0q0 = q0*q0;
float q0q1 = q0*q1;
float q0q2 = q0*q2;
float q0q3 = q0*q3;
float q1q1 = q1*q1;
float q1q2 = q1*q2;
float q1q3 = q1*q3;
float q2q2 = q2*q2;
float q2q3 = q2*q3;
float q3q3 = q3*q3;
// 测量归一化
norm = invSqrt(axf*axf + ayf*ayf + azf*azf);
axf = axf * norm; //向量a 为传感器重力 飞行器分量
ayf = ayf * norm;
azf = azf * norm;
// norm = invSqrt(mxf*mxf + myf*myf + mzf*mzf);
// 向量m 为传感器磁场 飞行器分量
// mxf = mxf * norm;
// myf = myf * norm;
// mzf = mzf * norm;
// 计算参考磁通方向
// hx = 2*mxf*(0.5 - q2q2 - q3q3) + 2*myf*(q1q2 - q0q3) + 2*mzf*(q1q3 + q0q2);//向量h 为磁场通过旋转以后 参考系分量
// hy = 2*mxf*(q1q2 + q0q3) + 2*myf*(0.5 - q1q1 - q3q3) + 2*mzf*(q2q3 - q0q1);
// hz = 2*mxf*(q1q3 - q0q2) + 2*myf*(q2q3 + q0q1) + 2*mzf*(0.5 - q1q1 - q2q2);
// bx = 1.0f/invSqrt((hx*hx) + (hy*hy));
//原则上应该只有X向的分量 ex的磁场传感器部分误差就是由此式产生。
// bz = hz;
//估计方向的重力和磁通（V和W）
//反向使用 四元数 及把a用-a替换。
vx = 2*(q1q3 - q0q2);
//v为把重力反向旋转到飞行器参考系时重力的向量
vy = 2*(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
// wx = 2*bx*(0.5 - q2q2 - q3q3) + 2*bz*(q1q3 - q0q2);
// w为把磁场反向旋转到飞行器参考系时磁场的向量
// wy = 2*bx*(q1q2 - q0q3) + 2*bz*(q0q1 + q2q3);
// wz = 2*bx*(q0q2 + q1q3) + 2*bz*(0.5 - q1q1 - q2q2);
// 错误是跨产品的总和之间的参考方向的领域和方向测量传感器 //建立误差函数 向量的外积
// ex = (ayf*vz - azf*vy) + (myf*wz - mzf*wy);
// ey = (azf*vx - axf*vz) + (mzf*wx - mxf*wz);
// ez = (axf*vy - ayf*vx) + (mxf*wy - myf*wx);
ex = (ayf*vz - azf*vy);
ey = (azf*vx - axf*vz);
ez = (axf*vy - ayf*vx);
halfT=getCurrentTime(timer4);
if (halfT>0.05)halfT=0;
// printf("%f\n\r",halfT);
if(ex != 0.0f && ey != 0.0f && ez != 0.0f)
{
// 积分误差比例积分增益
exInt = exInt + ex*Ki*(halfT);
eyInt = eyInt + ey*Ki*(halfT);
ezInt = ezInt + ez*Ki*(halfT);
// 调整后的陀螺仪测量
gxf = gxf + Kp*ex + exInt;
gyf = gyf + Kp*ey + eyInt;
gzf = gzf + Kp*ez + ezInt;
}
// halfT=getCurrentTime();
//printf("%f \n\r", halfT);
// 整合四元数率和归一化
//龙格-库格法
q0 = q0 + (-q1*gxf - q2*gyf - q3*gzf)*halfT;
q1 = q1 + (q0*gxf + q2*gzf - q3*gyf)*halfT;
q2 = q2 + (q0*gyf - q1*gzf + q3*gxf)*halfT;
q3 = q3 + (q0*gzf + q1*gyf - q2*gxf)*halfT;
// 归一化四元数
norm = invSqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 * norm;
q1 = q1 * norm;
q2 = q2 * norm;
q3 = q3 * norm;
} 与第二篇相比，算法中注释掉了所有与磁场有关的部分。
姿态更新后，用如下语句与磁场传感器计算出来的YAW(偏航角)进行混合
eulerAngleRaw.yaw = 0.9 * (eulerAngleRaw.yaw - gzF*2*halfT) + 0.1 * angleMagYaw; 经过检验，该算法姿态稳定，准确，变化迅速，YAW的值也能长期保证稳定，能为四轴飞行器提供很好的姿态数据
沙发，楼主好给力，赞一个！{:5_168:} 赞一个先。 什么时候完结 我好打包处理 哈哈 我出了个差，回来又出第三季了，哈哈，系列大片
页:
[1]