|
12023| 0
|
基于micropython的FIR滤波器(一) |
本帖最后由 1002victor 于 2017-12-27 16:47 编辑 FIR(Finite Impulse Response)滤波器:有限长单位冲激响应滤波器,又称为非递归型滤波器,是数字信号处理系统中最基本的元件,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。 ——————来自百度百科 本帖是继昨天发的一个滤波器帖子的系列帖 FIR滤波器是比较常用的一种数字滤波器,研究了两天了猝死不少脑细胞,作为一个开发人员讲究实用为主,钻太深的理论不是很擅长,现在对大致的原理和使用有了一个基本的了解,还没到达精通的地步,如有这方面的专家还请多多指教:handshake 本帖实验是基于pyboard的,原码作者是英国一个大牛用汇编写的https://github.com/peterhinch/micropython-filters.git 接下来主要对其进行测试顺便介绍这个滤波器的使用方法,后续会发两篇帖子具体介绍python语言的实现以及如何设计一个满足我们要求的滤波器 废话不多说,正式开始 首先弄明白他是用来干啥的 滤波 他有什么特殊之处 滤波滤的好  我说的是废话,但有这两条就足够成为我们认识他的原因了  在正式介绍之前先普及几个常识 不要管为什么,记住这是科学常识就好了 1.任何信号都是可以由由很多个不同频率不同幅值的三角函数来组合表示的 2.滤波的实质就是从这很多个不同的信号里把没用的信号剔除掉 有了上面两个常识我就要贴图了 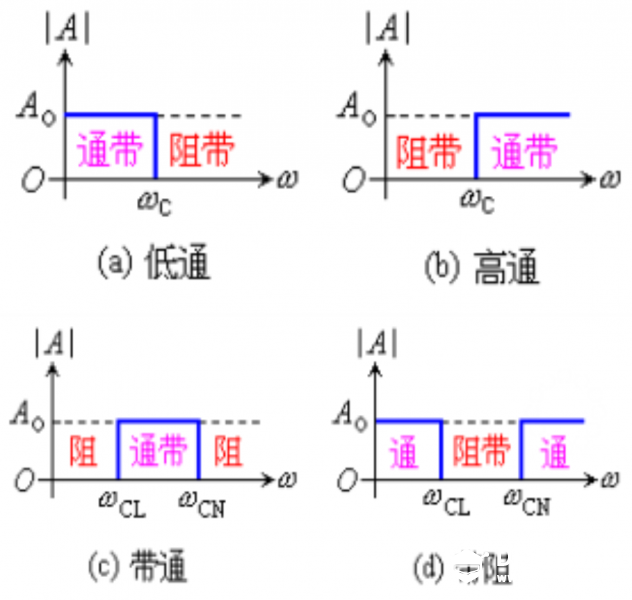 低通滤波器高通滤波器带通滤波器带阻滤波器这些概念相信大家都听过吧,低通滤波器就是低频率的信号可以通过高频率的信号被阻止,带通滤波器就是中间某一段频率带的信号可以通过,其他的被阻止,其余两种同理。通过的概念就是那个频率所对应信号的幅值不受影响,组织的概念的就是那个频率所对应信号的幅值被衰减为零,现在看上面那张图就很明朗了,横轴是频率,纵轴是幅值 那么我们滤波的过程就是根据我们的需要构造出上述四种基本的滤波器,现在FIR滤波器要上场了,因为它可以胜任这个工作 FIR滤波器说白了就是对N个样本数据执行加权和平均处理(专业叫卷积) 为了达到接地气喜闻乐见大部分人能看懂,太过于专业的词汇以及理论这里尽量不讲,但是有一些基本的词汇有必要先罗列出来,不然不好意思跟别人说你弄过FIR滤波器;P 1、抽头(Tap) - FIR的抽头是系数或者延时对.FIR抽头的个数(通常用N来表示)意味着:1)实现滤波器所需要的存储空间, 2) 需要计算的数目, 3) 滤波器能滤掉的数量, 实际上,越多的抽头意味着有更多的阻带衰减, 更少的波纹,更窄的滤波等等. 2、乘累加 (MAC) - 在FIR方面考虑,MAC是指把延时的数据采样与相应的系数相乘,然后累加结果。通常,FIR每一个抽头都需要一个MAC。 3、跃迁带(Transition Band) -在通带和阻带边沿之间的频带。跃迁带越窄,需要更多的抽头去实现滤波器。 下图是一个三抽头滤波器的示意图,结合图可以明白上面三个概念 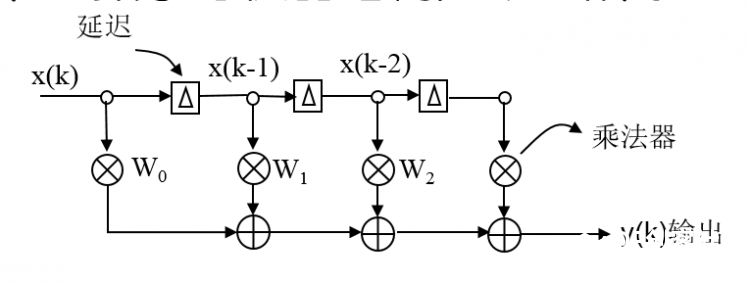 那么通用的一个N抽头的FIR滤波器的结构图如下图 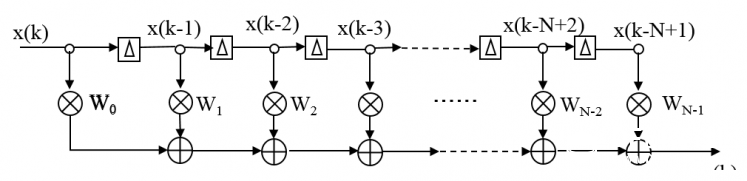 他可以实现的效果如下图所示, 如果是低通的就是可以把信号里面高频震荡统统滤除掉 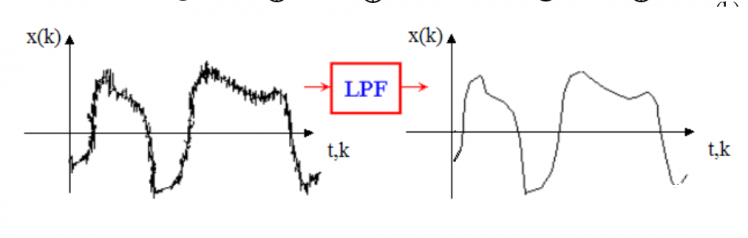 如果是高通的就是可以把信号里面低频信号统统滤除掉 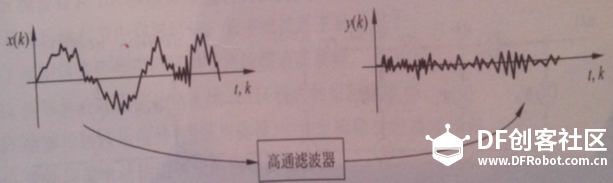 我们设计的滤波器的主要工作就是适当的选取W0到WN-1的系数使得滤波器达到我们的要求(原理很简单,但这个是重点!!!!!) 有了以上基础对FIR滤波器是啥能干啥也会有个基本的认识了,这个帖子我们先开始学习学习别人的代码,看看那个大牛写的代码怎么使用,后续发帖怎么设计 这位大牛代码仍然使用汇编写的 [mw_shl_code=python,true]# Implementation of FIR filter in Arm Thumb assembler # Author: Peter Hinch # 15th Feb 2015 # Updated to reflect support for push and pop # Calculate coefficients here: http://t-filter.appspot.com/fir/index.html # Function arguments: # r1 is an integer array of coefficients # r0 is an integer scratchpad array. Must be of length 3 greater than the # of coefficients. # Entry: # array[0] must hold the array length # array[1] the number of bits to scale (right shift) the result (0-31). # other elements must be zero # Run conditions # array[2] holds the insertion point address # r2 holds the new data value # Register usage (Buffer) # r0 Scratchpad # r2 new data value # r3 ring buffer start # r4 insertion point (post increment) # r5 last location in ring buffer # Register usage (filter) # r0 accumulator for result # r1 coefficient array # r2 current coeff # r3 ring buffer start # r4 insertion point (post increment) # r5 last location in ring buffer # r6 data point counter # r7 curent data value # r8 scaling value @micropython.asm_thumb def fir(r0, r1, r2): push({r8}) ldr(r7, [r0, 0]) # Array length mov(r6, r7) # Copy for filter mov(r3, r0) add(r3, 12) # r3 points to ring buffer start sub(r7, 1) add(r7, r7, r7) add(r7, r7, r7) # convert to bytes add(r5, r7, r3) # r5 points to ring buffer end (last valid address) ldr(r4, [r0, 8]) # Current insertion point address cmp(r4, 0) # If it's zero we need to initialise bne(INITIALISED) mov(r4, r3) # Initialise: point to buffer start label(INITIALISED) str(r2, [r4, 0]) # put new data in buffer and post increment add(r4, 4) cmp(r4, r5) # Check for buffer end ble(BUFOK) mov(r4, r3) # Incremented past end: point to start label(BUFOK) str(r4, [r0, 8]) # Save the insertion point for next call # *** Filter *** ldr(r0, [r0, 4]) # Bits to shift ?????????? mov(r8, r0) mov(r0, 0) # r0 Accumulator label(FILT) ldr(r7, [r4, 0]) # r7 Data point (start with oldest) add(r4, 4) cmp(r4, r5) ble(NOLOOP1) mov(r4, r3) label(NOLOOP1) ldr(r2, [r1, 0]) # r2 Coefficient add(r1, 4) # Point to next coeff mul(r2, r7) mov(r7, r8) asr(r2, r7) # Scale result before summing add(r0, r2, r0) sub(r6, 1) bpl(FILT) pop({r8}) [/mw_shl_code] 里面只有一个fir函数,这个函数作者做了很详细的描述,我再用自己的理解用汉语表达一下 三个入口参数 第一个是数据缓存区,同样根昨天滑动平均滤波一样,这个数据缓存的长度要比样本数量长度长3,缓存的第一个元素是样本的长度,是我们初始化的时候需要赋值的,第二个元素是对结果右移的位数,第三个是新元素插入的点(这个我们不需要操心) 第二个参数就是W系数数组了 第三个是新的采样数据 返回值是滤波以后的数据 用法: 由于该滤波器原理的特殊性,请务必保持每次调用的时间间隔是一致的!!!! 首先把符合我们需求的W系数写好 然后初始化样本缓存序列D,记得D长度要比W的长度长三,接着对缓存序列的第一个元素复制,值为样本的长度(也相当于W的长度),第二个元素为结果的变换尺度。 最后就可以周期性调用这个函数了fir(D,W,new_data) 下面跑一下原作者的测试函数测试一下程序耗时 [mw_shl_code=python,true]# Test functions for FIR filter import array import pyb from fir import fir # Coefficient options # 41 tap low pass filter, 2dB ripple 60dB stop c = [-176, -723, -1184, -868, 244, 910, 165, -1013, -693, 977, 1398, -615, -2211, -257, 3028, 1952, -3729, -5500, 4201, 20355, 28401, 20355, 4201, -5500, -3729, 1952, 3028, -257, -2211, -615, 1398, 977, -693, -1013, 165, 910, 244, -868, -1184, -723, -176] # 21 tap LPF d = [-1318, -3829, -4009, -717, 3359, 2177, -3706, -5613, 4154, 20372, 28471, 20372, 4154, -5613, -3706, 2177, 3359, -717, -4009, -3829, -1318] # 109 tap LPF e = [-24, 89, 69, 78, 95, 115, 135, 154, 171, 185, 196, 202, 201, 194, 178, 155, 122, 81, 31, -26, -91, -160, -232, -306, -378, -446, -506, -555, -591, -610, -608, -584, -535, -460, -357, -225, -66, 121, 333, 568, 823, 1094, 1375, 1663, 1952, 2237, 2510, 2768, 3004, 3213, 3391, 3534, 3638, 3702, 3723, 3702, 3638, 3534, 3391, 3213, 3004, 2768, 2510, 2237, 1952, 1663, 1375, 1094, 823, 568, 333, 121, -66, -225, -357, -460, -535, -584, -608, -610, -591, -555, -506, -446, -378, -306, -232, -160, -91, -26, 31, 81, 122, 155, 178, 194, 201, 202, 196, 185, 171, 154, 135, 115, 95, 78, 69, 89, -24] # Initialisation coeffs = array.array('i', e) ncoeffs = len(coeffs) data = array.array('i', [0]*(ncoeffs +3)) data[0] = ncoeffs data[1] = 1 # Try a single bit shift def test(): # Impulse response replays coeffs*impulse_size >> scale print(fir(data, coeffs, 100)) for n in range(len(coeffs)+3): print(fir(data, coeffs, 0)) def timing(): # Test removes overhead of pyb function calls t = pyb.micros() fir(data, coeffs, 100) t1 = pyb.elapsed_micros(t) t = pyb.micros() fir(data, coeffs, 100) fir(data, coeffs, 100) t2 = pyb.elapsed_micros(t) print(t2-t1,"uS") # Results: 14uS for a 21 tap filter, 16uS for 41 taps, 23uS for 109 (!) # Time = 12 + 0.102N uS where N = no. of taps test() print("Done! Timing:") timing() [/mw_shl_code] 109抽头耗时22微秒,测试代码里放了三组低通滤波器的系数,一组21抽头,一组41抽头,还有109抽头的。不同抽头的耗时是不一样的,作者在代码注释部分有说明,这里就不在重复测试了。 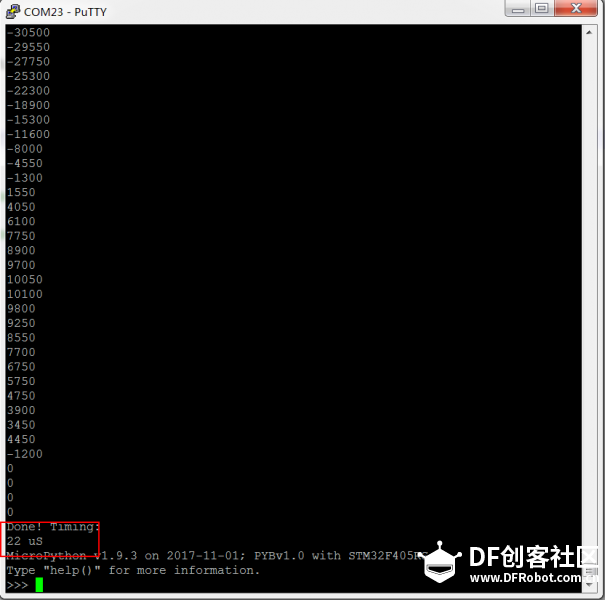 作者的代码里面还有一个lpf.py和osc.py的测试代码,分别为低通滤波器带通滤波器的测试代码 代码的思路是通过pyboard的DAC产生一个扫频正弦波,频率的起止范围以及步进值可以任意设置,然后通过ADC采集滤波器滤波处理后另外一路DAC输出。 产生正弦波的是DAC1在X5引脚,ADC采集是X7引脚,滤波输出是X6引脚,测试的时候把X5和X7连接起来,可以用双通道示波器观察X5和X6输出的波形。 我就用文字描述一下测试现象吧,因为当时测试时没录视频,现在示波器不在手头:lol lpf.py通过0-40Hz低频信号,在示波器里可以看出当下X5的信号处于0-40Hz时X6引脚有一样的信号输出,波形有稍微的延迟,当X5的频率逐渐升高时X6的波形逐渐变小直到输出为零。 osc.py是选择性通过100Hz信号,在示波器里可以看出当下X5的信号在100Hz左右是时X6引脚有信号输出,当X5的信号为100Hz时X6波形和X5一样,有稍微的延迟,其余频率X6的波形逐输出都为零。 当然我们可以通过把数据从串口发送出去,然后用串口示波器显示出来的办法,但是在实践过程中由于这个滤波器的原理所决定其每一步采样的时长间隔必须一致,所以程序是在定时中断里实现的,当我把串口发送放在里面是出现了内存不够用的错误,我把micropython.alloc_emergency_exception_buf(100)数字改大也不行,进过一番周折多加了yi个定时器把程序做了一定的修改勉强实现了这个想法。正弦波的频率从10赫兹以10赫兹递增到120赫兹,没1.25s递增一次。代码如下 [mw_shl_code=python,true]import protocol import math import pyb import array from fir import fir import micropython micropython.alloc_emergency_exception_buf(100) # Define hardware dac1 = pyb.DAC(1) dac2 = pyb.DAC(2) adc = pyb.ADC("X7") tim = pyb.Timer(4, freq=2000) # Sampling freq 10KHz is about the limit 14KHz without constraint tim2 = pyb.Timer(1, freq=0.8) uart_port = pyb.UART(4,57600) # Data for FIR filter Pass (@2Ksps) 0-40Hz Stop 80Hz-> coeffs = array.array('i', (72, 47, 61, 75, 90, 105, 119, 132, 142, 149, 152, 149, 140, 125, 102, 71, 33, -12, -65, -123, -187, -254, -322, -389, -453, -511, -561, -599, -622, -628, -615, -579, -519, -435, -324, -187, -23, 165, 375, 607, 855, 1118, 1389, 1666, 1941, 2212, 2472, 2715, 2938, 3135, 3303, 3437, 3535, 3594, 3614, 3594, 3535, 3437, 3303, 3135, 2938, 2715, 2472, 2212, 1941, 1666, 1389, 1118, 855, 607, 375, 165, -23, -187, -324, -435, -519, -579, -615, -628, -622, -599, -561, -511, -453, -389, -322, -254, -187, -123, -65, -12, 33, 71, 102, 125, 140, 149, 152, 149, 142, 132, 119, 105, 90, 75, 61, 47, 72)) ncoeffs = len(coeffs) data = array.array('i', [0]*(ncoeffs +3)) # Scratchpad must be three larger than coeffs data[0] = ncoeffs data[1] = 16 start = 10 end = 120 step = 10 freq = start buf = bytearray(100) for i in range(len(buf)): buf = 128 + int(110 * math.sin(2 * math.pi * i / len(buf))) out_val = 0 in_data = 0 send_data = bytearray(9) uart_port.write(send_data) # Data input, filter and output # The constraint is a convenience to ensure that any inadvertent overflow shows as # clipping on the 'scope. If you get the scaling right you can eliminate it... def cb(timer): global in_data,out_val in_data = adc.read() out_val = fir(data, coeffs,in_data) // 16 # Filter amd scale dac2.write(max(0, min(255, out_val))) # Constrain, shift (no DC from bandpass) and output def send(timer): global freq,start,end, mult,buf freq += step if freq > end: freq = start dac1.write_timed(buf, int(freq) * len(buf), mode=pyb.DAC.CIRCULAR) print(freq, "Hz") tim.callback(cb) tim2.callback(send) while True: send_data = protocol.data_send(in_data//16,out_val,0,0,0,0,0,0,0) uart_port.write(send_data) pyb.udelay(500)[/mw_shl_code] 结果如下,红色是原始的扫频正弦波信号,蓝色的是滤波以后输的的信号,大致可以看出前面低频部分两者信号是基本一致的,随着信号频率的增加,蓝色的开始衰减直到最后为零 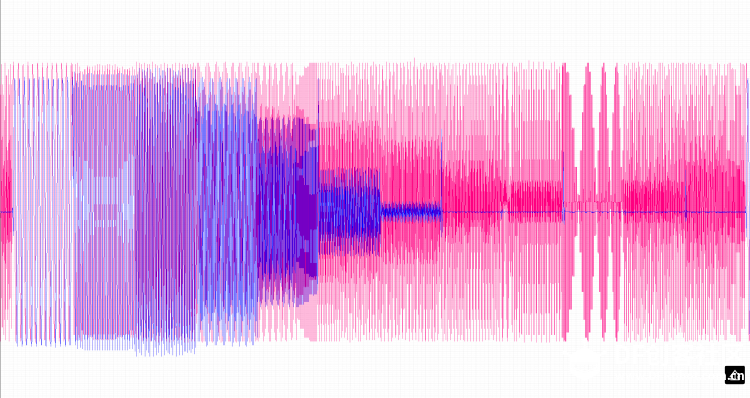 这是10Hz,20Hz,30Hz,40Hz四段的(频率是以10递增的) 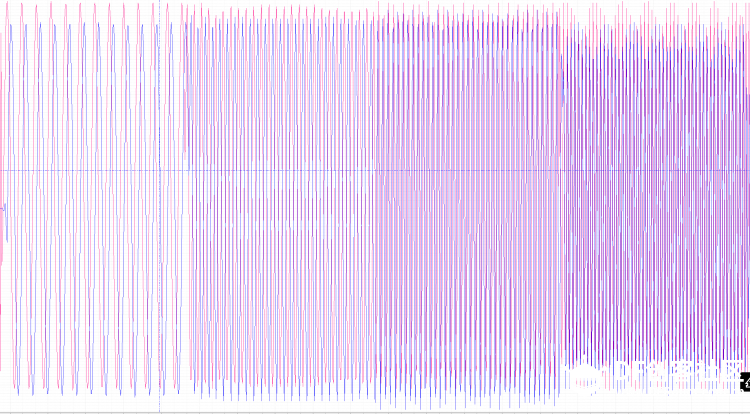 这是40Hz,50Hz,60Hz,70Hz四段的,可以看40以后已经开始衰减了  这是70hz以后的,已经衰减为零了 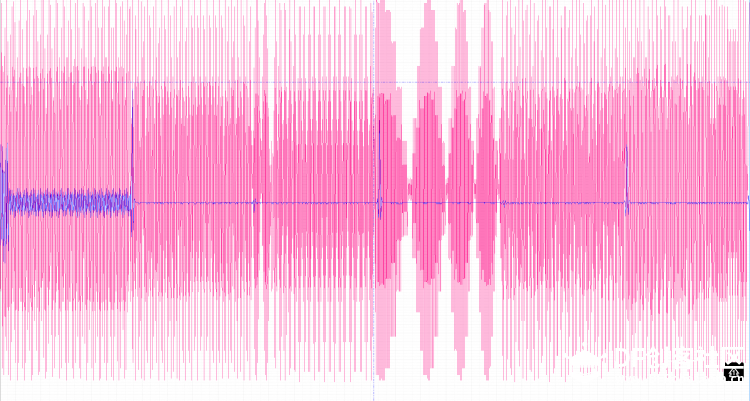 来一张10Hz的放大图,可以看出,波形有稍微的延迟,前面是有一小段120hz的,由于采样率的原因红色原始波形虽有失真但是可以看出蓝色滤波后的信号输出为零的 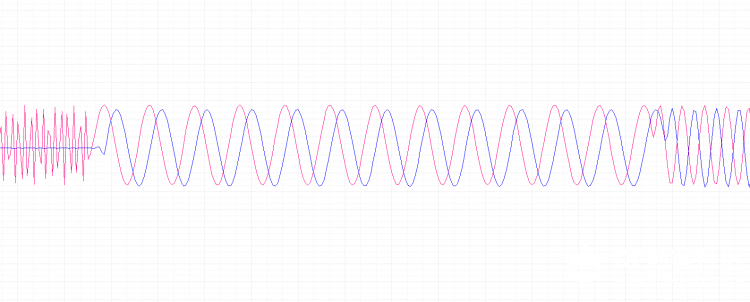 到此,FIR滤波器的测试已经完成,帖子中如有疏漏欢迎指教。 |
 沪公网安备31011502402448
沪公网安备31011502402448© 2013-2026 Comsenz Inc. Powered by Discuz! X3.4 Licensed