基于Arduino的离散傅里叶变换测试

在物理实验中时常需要记录周期性运动的数据，为了得到其周期，可以导入python或其他程序进行离散傅里叶分析。

不过，每次都导入其他程序分析总显得麻烦，故本帖尝试寻找一种方法，让单片机自己记录好数据后自动找到周期性运动的频率。


经测试，一般UNO或pro mini类存储空间不够，故改用Seeed Studio XIAO nRF52840 Sense

官网见：https://wiki.seeedstudio.com/XIAO_BLE/

#include <avr/pgmspace.h>
#include <math.h>

#define N 256 // Number of samples for DFT

double real[N];
double imag[N];

void setup() {
  Serial.begin(9600);
  while (!Serial) {
    ; // Wait for serial port to connect
  }
}

void loop() {
  // Read analog input from A0
  for (int i = 0; i < N; i++) {
    double val = cos(2.0 * M_PI * 8.0 * i/255.0); //生成一个频率为8Hz的信号，时间长度为1秒
    real[i] = val; // Store sample in the real array
    imag[i] = 0; // Initialize imaginary part to 0
  }
  
  // Perform DFT
  for (int k = 0; k < N; k++) {
    double sumReal = 0;
    double sumImag = 0;
    
    for (int t = 0; t < N; t++) {
      double angle = 2 * M_PI * t * k / N;
      sumReal +=  real[t] * cos(angle) + imag[t] * sin(angle);
      sumImag += -real[t] * sin(angle) + imag[t] * cos(angle);
    }
    
    // Normalize the result
    double magnitude = sqrt(sumReal * sumReal + sumImag * sumImag) / N;
    
    // Output the magnitude to the serial monitor
    Serial.print(k);
    Serial.print("\t");
    Serial.print(magnitude);//输出频谱纵轴
    Serial.print("\t");
    Serial.println(real[k]); //输出原始周期信号
  }
  
  delay(5000); // Delay for 5 second before the next measurement
}
复制代码

类似于示波器切片输出，单片机每256个数据后等待5秒，方便复制序列窗口的内容到Excel测试。结果如下：

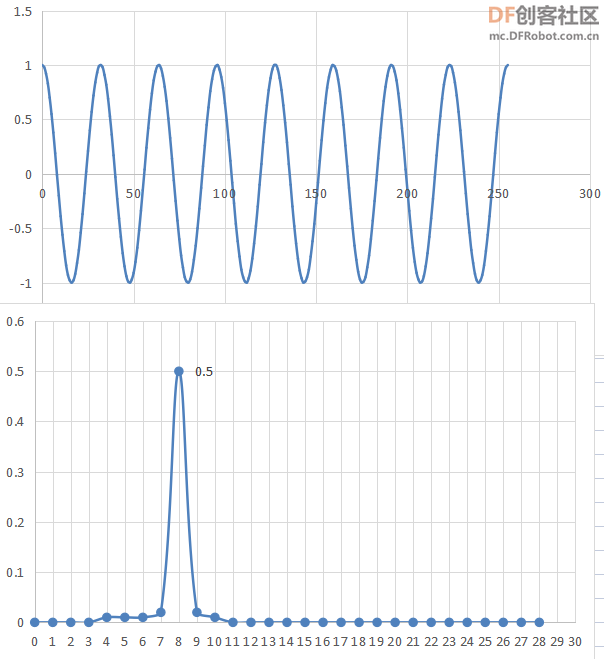
值得关注的是，自生成的256个元素的数组，默认为1s内记录的数据。数学中频率为f的余弦函数基础表达式为: cos(2 * pi * f * t )
代码中 cos(2.0 * M_PI * 8.0 * i/255.0) 意为i从0到255，t 自0到1.


最后发现，确实在8Hz处出现峰值，验证成功。

=================================================================

2023/7/8更新

尝试使用XIAO SENSE自带的三轴加速度传感器来测试，方便起见，只用Z轴（垂直于板平面）。
在插着数据线状态下，像扇扇子一样挥动XIAO SENSE，如图：

#include <avr/pgmspace.h>
#include <math.h>

#include "LSM6DS3.h"
#include "Wire.h"

LSM6DS3 myIMU(I2C_MODE, 0x6A);    //I2C device address 0x6A

#define N 256 // Number of samples for DFT
float real[N];
float imag[N];
unsigned long start_t;

void setup() {
  Serial.begin(9600);
  while (!Serial) {
    ; // Wait for serial port to connect
  }
  if (myIMU.begin() != 0) {
    //Serial.println("Device error");
  }
  else{
    //Serial.println("Device OK!");
  }
}

void loop() {
  start_t = millis();
  for (int i = 0; i < N; i++) {
    //float val = cos(2.0 * M_PI * 8.0 * i/255.0 * 2.0);
    float val = myIMU.readFloatAccelZ();
    real[i] = val; // Store sample in the real array
    imag[i] = 0; // Initialize imaginary part to 0
    delay(20);//每20ms记录一个数据，总计duration 255*20ms = 5100ms = 5.1s
  }
  Serial.println( millis() - start_t );
  // Perform DFT
  for (int k = 0; k < N; k++) {
    float sumReal = 0;
    float sumImag = 0;
    
    for (int t = 0; t < N; t++) {
      float angle = 2 * M_PI * t * k / N;
      sumReal +=  real[t] * cos(angle) + imag[t] * sin(angle);
      sumImag += -real[t] * sin(angle) + imag[t] * cos(angle);
    }
    
    // Normalize the result
    float magnitude = sqrt(sumReal * sumReal + sumImag * sumImag) / N;
    
    // Output the magnitude to the serial monitor
    Serial.print(k);
    Serial.print("\t");
    Serial.print(magnitude);
    Serial.print("\t");
    Serial.println(real[k]);
  }
  
  delay(5000); // Delay for 1 second before the next measurement
}
复制代码

慢速甩动测试：

视频地址：链接: https://pan.baidu.com/s/1Mu1BhBEesIPPW_tndhoTRQ?pwd=8888 提取码: 8888


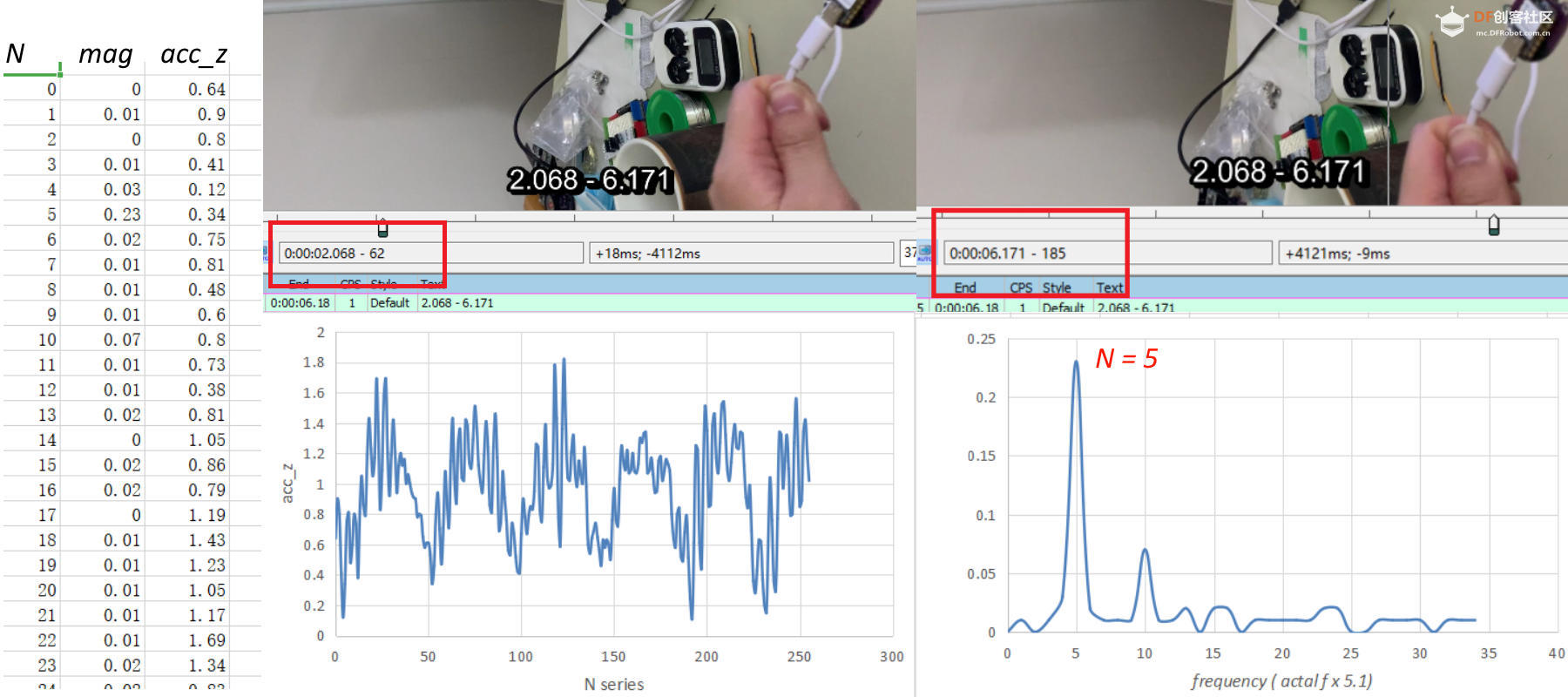
取4次甩动周期，时间自2.068 s 到 6.171 s，

时长4.103 s

平均周期取四位有效位数为

4.103 / 4 = 1.026 s

理论频率为0.9749 Hz。

记录的数据分析结果如上图：

左图为Z轴加速度数据，右图为傅里叶变换后结果：

#偶尔第一行N = 0 时数值很高，可以改为0。

根据结果，显示峰值在N = 5。

假定每次记录的数据间隔仅20ms，则记录256个数据总时长为255 * 20 ms = 5100 ms = 5.1 s
（见代码delay设定，实际总duration 应大于5.1s）


原代码中256个数据默认为1秒内记录的数据（见上例），故图中峰值5Hz应该缩小5.1倍

修正：
5  / 255 / 0.02  = 5 / 5.1 = 0.98 Hz


相较于理论频率 0.9749Hz 已非常接近。

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

快速甩动测试：

视频地址：链接: https://pan.baidu.com/s/1UOCqrCCBoUgybaMapF1avA?pwd=8888 提取码: 8888


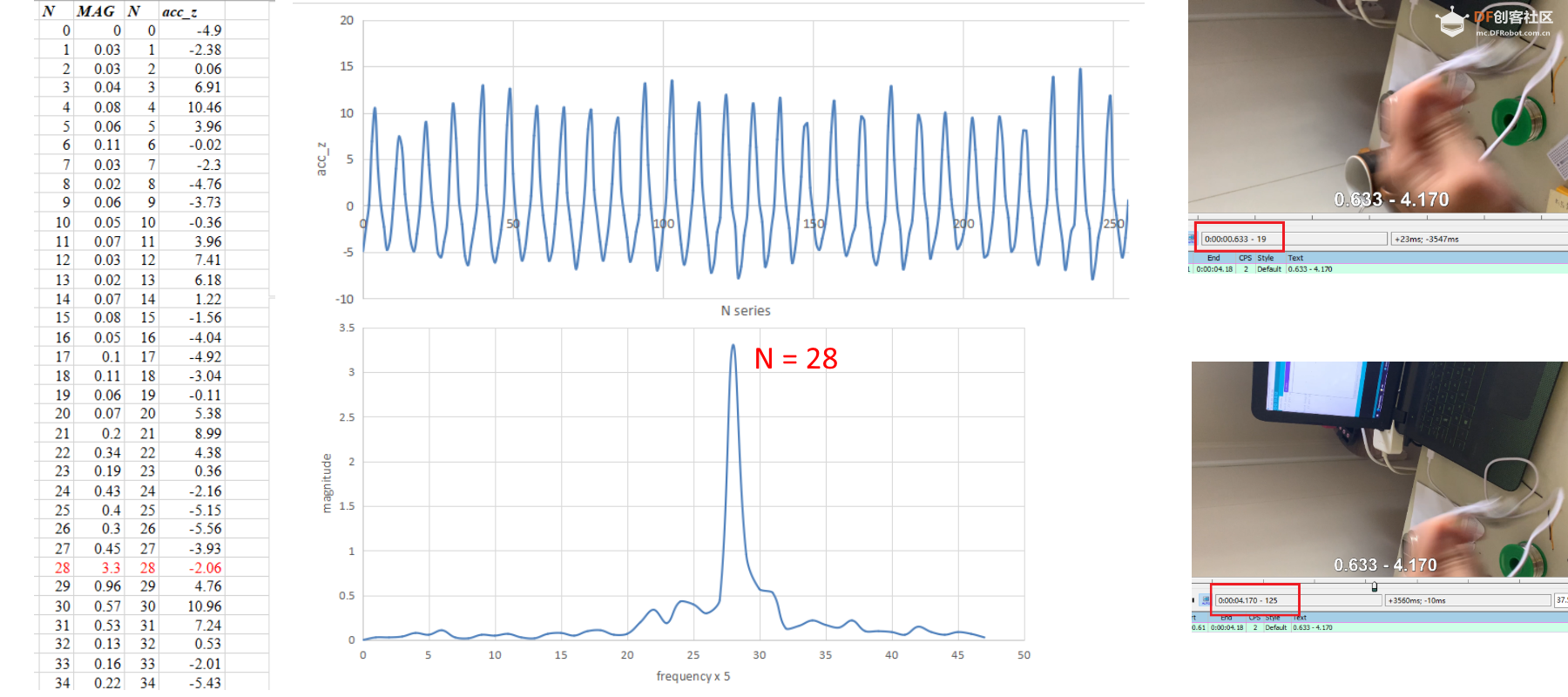
取20次甩动周期，时间自0.633 s 到 4.170 s，

时长3.537 s

平均周期取四位有效位数为

3.537 / 20 = 0.177 s

理论频率为5.655 Hz。


记录的数据分析结果如上图：

左图为Z轴加速度数据，右图为傅里叶变换后结果：

根据结果，显示峰值在N = 28.

修正：
28  / 255 / 0.02  = 28 / 5.1 = 5.49 Hz


相较于理论频率 5.655Hz 略小，误差2.9%。

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

【值得继续讨论的内容】
1. 对于高频信号的处理可行性；
2. 验证复杂信号的适用性；3. 实际数据记录时间是否大于或小于5.1s；

厉害厉害

赞赞赞赞赞