|
20262| 16
|
[项目] 球-杆系统 从硬件到算法 |

|
本帖最后由 饶厂长 于 2017-10-27 14:27 编辑 大家好, 饶厂长已经从上海回到自己的工作室, 在机器被击败后痛定思痛,决定做更多东西, 学更多技术。 今天撰写一个球杆系统的软件与硬件设计教程,意在展示一个控制算法项目的一般内容。 前言:什么是球杆系统 在放上大量的公式和框图之前, 先放个动图
figure 0.1 球杆系统动态运行动图 如图所示, 在平杆的任何初始位置下, 小球最终都能向设定点位置移动,并能够抵抗小的扰动, 将小球保持在设定点。 可以看到, 通过电机来控制杆的角都, 从而影响小球的运动方向, 这就是我们所面对的运动对象, 球杆系统。 换句话来说, 球杆系统中我们想要控制的是: 小球在横杆上的相对位置。在球杆系统中, 我们能直接控制的是: 电机的运转速度与方向。从这两句话中, 我们已经可以得出被控系统的系统框图了。
figure 0.2 球杆系统框图 将电机转速与小球位置直接联系起来是很困难的, 很少有人能够直观精准的想象出来, 就像很少有人能直观精准的想像到发动机进气量对位移的影响。但当我们将这个对象拆解开来, 就变得更加直观容易了。 我们可以想象到, 电机转速对横杆角度的影响, 也可以想象到横杆角度对小球的加速度影响, 从加速度我们可以想象小球的速度变化趋势, 从速度变化趋势我们能够估计出小球的位移。我们一个个来看, 电机转速到横杆角度, 实际上就是一个简单的积分器。横杆角度到小球的加速度, 存在一个非线性关系。 加速度到速度貌似是个积分关系, 但因为阻力速度不会无界的增加, 加速度会随速度增大而减小。 实际上在本系统中速度比较小, 可以简化为积分环节。最终的环节, 速度到位移, 是单纯的积分关系。 那么figure0.2的框图就可以简化分解为如下。
第二章: 角度控制器设计 不同于普通的直流电机, 输入电压输出转速, 步进电机是输入脉冲, 输出角度变化, 换言之, 也可以是输入单位时间的脉冲, 输出单位时间的角度变化, 其实就是转速。 我们可以通过控制脉冲的频率控制电机转速, 通过脉冲的顺序控制电机的转向。makeblock的步进电机驱动替我完成了脉冲控制的部分, 我只需要提供一个PWM信号作为脉冲, 一个电平信号作为转向即可。 PWM的频率能够控制电机的转速关于PWM的频率变化, 需要通过配置寄存器来改变内部定时器的设定。在这里我使用了Arduino PWM library, 该库具有改变PWM频率的功能。该库提供了一个直接改变指定引脚方波频率的函数, 直接使用即可。 配置方法如下: [mw_shl_code=applescript,true]#include <;PWM.h> 步进电机驱动有两个控制口, 一个链接在D11上, 给pwm脉冲信号,另一个接在D12上, 给高低电平, 控制转向。 编写电机运动代码: [mw_shl_code=applescript,true]void run_motor(int speed_value) { 这段函数的输入参数为设定速度, 实际上就是频率值。 根据实际测量, 当超过10000时, 电机就无法输出扭矩正常转动了, 故做一个饱和限制。 接下来检测一下旋转电位器的输出, 发现ad读数在363时横杆为水平状态。既然电机已经能够控制, 横杆的角度也可以检测, 接下来就该做一个控制器,让横杆按照期望的角度运动。控制框图如下:
figure 2.1 角度控制框图 使用最简单的反馈策略, 即控制什么反馈什么。 由于噪声和测量分辨率的限制,反馈回来的角度不可避免的具有误差。 反馈控制器采用PD, 可以避免系统超调震荡。 理论上说, 单纯的P控制即可, 并不应该产生震荡, 但实际上系统存在一定的惯性, 超调是不可避免的, 因此必须加入微分控制。 不加积分的原因是,被控系统本身含有积分环节, 能够避免稳态误差, 故不需要引入积分环节。 加入前馈的原因是, 前馈能够又快又好的跟踪变化的信号。 编写控制器的函数如下: [mw_shl_code=applescript,true]float position_loop(int set_point, int state, int velocity, float p, float i, float d) {float e, de; static float sum_e; float u; e = set_point - state; de = -velocity; sum_e += e; u = e * p + sum_e * i + de * d; return u; }[/mw_shl_code] 编写执行部分代码如下
[mw_shl_code=cpp,true]observed_speed = 20*dirivative_speed(363-desire_angle); 以上功能代码执行效果如下:
figure 2.2 角度控制效果 第三章: 小球运动系统辨识与观测器设计 在完成了角度控制之后, 整个系统的框图就变了。  figure 3.1 角度控制后系统框图 如图所示, 角度控制后, figure0.2的第一个子系统变成输入为角度设定了。 如果想要控制小球的位移, 我们可以进行一个位移的闭环控制。 同时, 可以将小球的运动的两次积分简化为单个系统(速度无法直接观测, 分为单个系统无意义)。  figure 3.2 位移控制策略 此时的控制框图是个典型的串级控制结构, 外环套内环。 此时系统的控制器设计与普通的二阶系统控制器设计毫无二致, 除了中间的非线性环节之外。 经过分析, 该非线性环节是一个关于y=sin(x)的函数, 在x绝对值比较小的时候可以近似为y=x, 因此该环节在系统中可直接忽略。 另外要注意的是, 对象是一个包含两个积分环节的二阶系统, 如果单纯使用P控制, 则系统极点在y轴,属于临界稳定, 理想状况下会震荡, 所以需要PD控制将极点配在坐标系左边。 另外系统无需积分即可消除稳态误差, 这是因为系统包含积分环节。 那么此时是否可以开始设计PD控制器了呢? 在设计之前, 得考虑位移误差的微分如何得到。 位移的微分其实就是速度值。 我们只有位移传感器, 却没有速度传感器, 那么此时就必须进行微分。 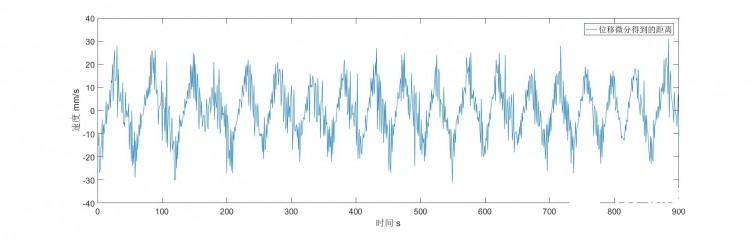 figure 3.3 位移微分的结果 如图所示, 直接微分的结果非常糟糕, 信噪比目测不足2:1, 在这种情况下控制器不光无法镇定, 高频的抖动还可能损坏机械结构。 现在有两个解决办法, 一是通过购买噪声非常小的激光测距传感器或其他传感器来获得更为理想的测量值,二是通过观测器的设计来替代微分, 获得较好的速度值。 接下来我会选择第二种方法解决这个问题。 观测器本质上是一种数据融合的方法, 将系统的动力学模型的预测值与测量值进行信息的融合, 获得更为平滑低噪声的信息。 著名的卡尔曼滤波就是观测器的一种动态的最优解。 在进行观测器设计之前, 我们至少需要大概计算一下系统的动力学模型, 这就是系统辨识。 简单的说, 观测器就是通过系统模型和观测值来估计观测值之外的状态量。 系统辨识就是通过系统的输入和输出计算系统的模型。 这个时候滑动变阻器就派上用场了。  figure 3.4 手操横杆控制 输入量即角度值, 输出量即位移值, 将手动控制过程中的数据提取出来, 利用matlab的系统辨识工具箱进行快速而简单的辨识。 模型阶次2阶, 模型类型选择观测标准型。 然后就能够得到辨识后的系统了。 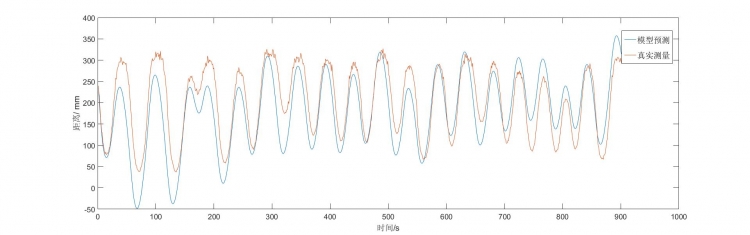 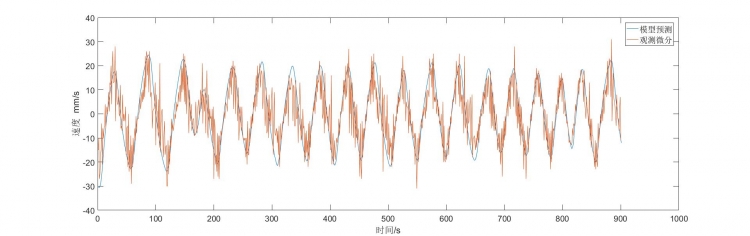 figure 3.5 辨识得到的模型对辨识数据的预测仿真 可以看到, 辨识的模型很精准的把握了位移的变化趋势, 但并没有和位移完全重合。 这是机械的摩擦、滑动造成的。 另外模型预测的速度信息比较平滑, 也很好的跟随了微分后的位移量。 观测器的设计其实就是设计A-LC这个矩阵的特征根。 我的系统是离散系统, 因此该特征根在极坐标下应该是在单位圆内的, 这才能保证观测器的收敛。 我经验的选取L使得特征根为[0.3016 0.6451]。 将观测器的形式与反馈L带入到观测模型中, 得到观测数据:  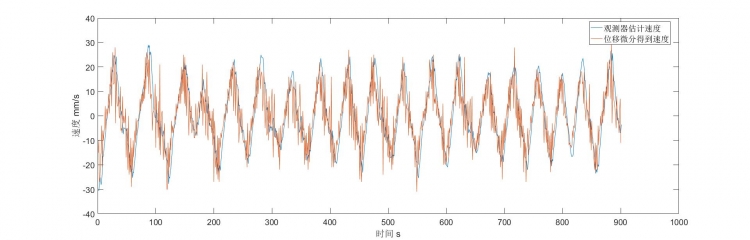 figure 3.6 观测结果 可以看到, 观测所得位移跟踪性能良好, 观测所得速度也比较平滑, 且没有漂移误差, 基本可以判定为该参数可用。 接下来就可以将观测模型移植到arduino代码中测试。 在线运行观测器代码如下: [mw_shl_code=cpp,true]float x1, x2, x1_new = 130, x2_new = 0; void observer(float u, float y, float dy) { x1 = x1_new; x2 = x2_new; x1_new = 0.0001 * x1 + 0.0487 * x2 - 0.1676 * u + y; x2_new = -3.969 * x1 + 0.9466 * x2 - 1.6475 * u + 4 * y; }[/mw_shl_code] 运行效果 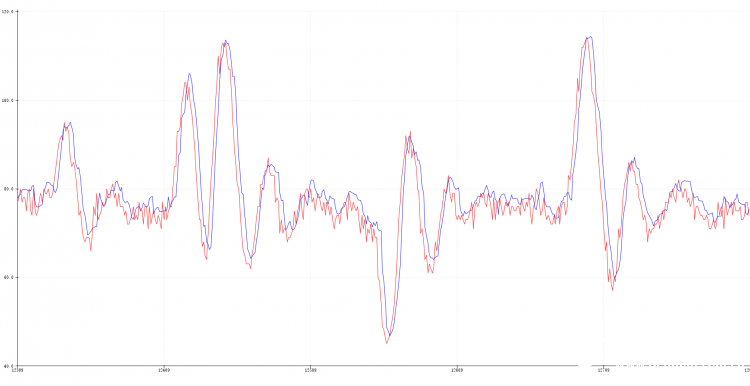 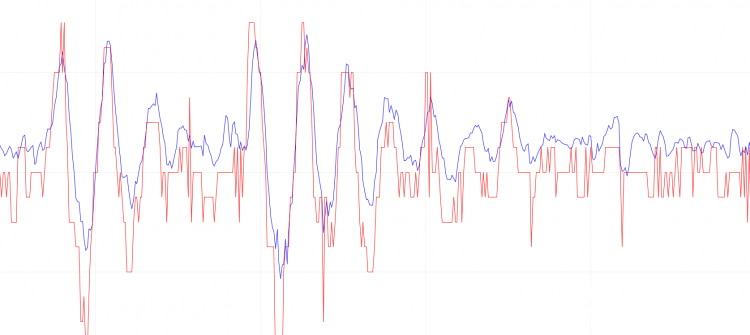 figure 3.7 左边是距离观测 右边是速度观测 可见观测结果跟踪性能良好, 有效滤去了微分带来的噪声。 在此基础上设计位移控制器, 代码如下: [mw_shl_code=cpp,true]float moving_loop(float set_point, float state, float velocity, float p, float i, float d) { float e, de; static float sum_e; float u; sum_e += set_point - state; u = (p * (set_point - state) + i * sum_e - d * velocity); return u; }[/mw_shl_code] 运行效果如下动图:  figure 3.7 左边是距离观测 右边是速度观测 figure 3.7 左边是距离观测 右边是速度观 figure 3.8 控制效果动图 可以看到, 稳态时并没有高频抖动产生, 这都得益于观测器的设计。 单点稳定抗扰的效果还是可以, 但是追踪的结果很一般, 因此没有放上追踪波形图。 第四章: 总结与反思 目前的系统性能很一般, 只能满足最基础的稳定在某一点的要求。 在追踪变化信号时存在震荡或卡死。 这主要还是源于滑物体与横杆的静态摩擦力较大造成的, 这一点可以通过将物体换成更为光滑的金属小球来解决。 另外横杆的平面也有凹凸, 给系统引入了一些鞍点。 此外, 角度检测的分辨率有待提高, 这也是通过硬件能够解决的问题。 等之后购买了新的小球、ad芯片和新的横杆后, 再进行进一步的调试。 虽然最终的结果差强人意, 但依然包含了控制中的基本问题, 包括建立模型, 串及控制设计, 前馈反馈控制, 检测, 数字滤波, 系统辨识, 观测器数据融合设计这几项内容。 通过做这个只想表达一点: 饶厂长是个合格的控制算法工程师, 就这样 |
 沪公网安备31011502402448
沪公网安备31011502402448© 2013-2026 Comsenz Inc. Powered by Discuz! X3.4 Licensed