|
11819| 2
|
[项目] 自两轮平衡车 |

|
本帖最后由 康康 于 2019-11-24 17:26 编辑 平衡车,年轻人都喜欢吧!大街上看着各式各样的人骑着平衡车在马路上穿梭,看上去赶紧还是挺拉风的,现在对于企业来说平衡车技术已经很成熟了,包括四轴也一样,大疆站在世界顶端。但是自己动手DIY一辆不知道有多少小伙伴感兴趣,反正我就是闲,约闲越折腾,啦啦啦啦~ 那么动手!先介绍下平衡车的原理。 双轮平衡车的想法来自于倒立摆模型,摆只能在平面运动,如果摆倒向左边,那么摆的底部就必须也向左边移动,以保持摆的竖直平衡,右边情况与左边类似。两轮自平衡小车的情况与倒立摆相似,也需要类似的运动来保持摆车架的竖直平衡。如图:  #系统组成 系统包括:第一是双轮平衡车的机械结构设计,由两轮平衡小车的机械结构搭建工作平台,承载硬件电路。其中包括车身上支架、下平台灯;第二十硬件电路设计,包含电源、单片机、传感器、电机等综合系统;第三十平衡控制模块,要求平稳,数据采集等;第四十双轮平衡车的软件设计,按要求写出看着程序,解决运动状态下如何保存平衡系统问题。 该系统主要实现3个部分:小车的硬件设计,一个好的硬件结构可以减少不必要的调试麻烦;第二十平衡信号检测,要求传感器检测系统要能快速检测倒倾斜信号,保证小车静止平衡和倾斜情况之后的调节能力;第三是单片机通过对检测倒的信号进行分析和处理,通过相应的程序来实现。 功能模块包括:传感器部分,三轴加速度传感器和陀螺仪等。为电机控制提供准确的速度方向反馈。MCU部分,最小系统模块和PWM电机驱动模块,使用单片机Arduino UNO,完成采集信号处理和控制信号输出。 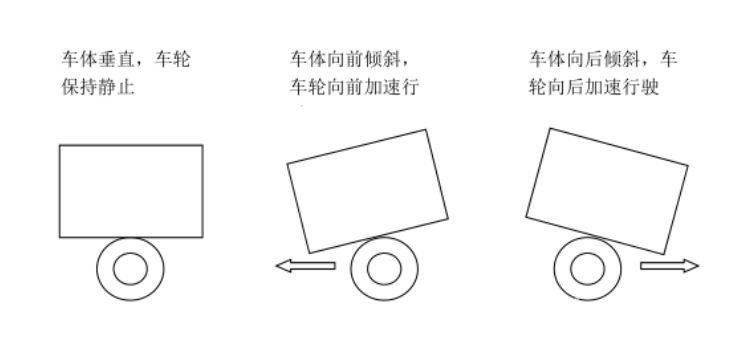 整体电路设计: 1)陀螺仪:一路,测量陀螺仪输出电压。 2)加速度计:一路,测量加速度Z轴输出电压 3)PWM:控制左右两个电机双方向运行,需要四路PWM接口。 4)通信接口I2C:读取陀螺仪加速度值 5)电机驱动:需要两个电机运行电路 驱动直流电机 本模块是2路的H桥驱动,可以同时驱动两个电机,是能ENA、ENB后,可以分别从IN1 IN2 IN3 IN4输入PWM信号驱动电机1和电机2的转速方向.   注意:如果L298和arduino不能同时供电的话,那么需要将arduino和298的GND接一起,这样单片机上过来的逻辑信号才有一个参考点0. MPU6050 MPU6050的数据接口用的是I2C总线协议,因此我们需要Wire程序库的帮助来实现Arduino和MPU6050之间的通信 Wire的官方库arduino.cc/en/Reference/Wire  在Github上找到卡尔曼滤波的程序 https://github.com/wjjun/MPU6050_Kalman) 把程序上传倒板子上,打开串口监视器,可以看到一堆数据 简单的陀螺仪读出数据 #include "Wire.h" #include "I2Cdev.h" #include "MPU6050.h" MPU6050 accelgyro; int16_t ax, ay, az; int16_t gx, gy, gz; bool blinkState = false; void setup() { Wire.begin(); Serial.begin(38400); accelgyro.initialize(); } void loop() { accelgyro.getMotion6(&ax, &ay, &az, &gx, &gy, &gz); Serial.print("a/g:\t"); Serial.print(ax); Serial.print("\t"); Serial.print(ay); Serial.print("\t"); Serial.print(az); Serial.print("\t"); Serial.print(gx); Serial.print("\t"); Serial.print(gy); Serial.print("\t"); Serial.println(gz); blinkState = !blinkState; } 什么是卡尔曼滤波 卡尔曼滤波一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。 传统的滤波方法,只能是在有用信号与噪声具有不同频带的条件下才能实现.20世纪40年代,N.维纳和A.H.柯尔莫哥罗夫把信号和噪声的统计性质引进了滤波理论,在假设信号和噪声都是平稳过程的条件下,利用最优化方法对信号真值进行估计,达到滤波目的,从而在概念上与传统的滤波方法联系起来,被称为维纳滤波。这种方法要求信号和噪声都必须是以平稳过程为条件。60年代初,卡尔曼(R.E.Kalman)和布塞(R.S.Bucy)发表了一篇重要的论文《线性滤波和预测理论的新成果》,提出了一种新的线性滤波和预测理由论,被称之为卡尔曼滤波。特点是在线性状态空间表示的基础上对有噪声的输入和观测信号进行处理,求取系统状态或真实信号。 这种理论是在时间域上来表述的,基本的概念是:在线性系统的状态空间表示基础上,从输出和输入观测数据求系统状态的最优估计。这里所说的系统状态,是总结系统所有过去的输入和扰动对系统的作用的最小参数的集合,知道了系统的状态就能够与未来的输入与系统的扰动一起确定系统的整个行为。 卡尔曼滤波不要求信号和噪声都是平稳过程的假设条件。对于每个时刻的系统扰动和观测误差(即噪声),只要对它们的统计性质作某些适当的假定,通过对含有噪声的观测信号进行处理,就能在平均的意义上,求得误差为最小的真实信号的估计值。因此,自从卡尔曼滤波理论问世以来,在通信系统、电力系统、航空航天、环境污染控制、工业控制、雷达信号处理等许多部门都得到了应用,取得了许多成功应用的成果。例如在图像处理方面,应用卡尔曼滤波对由于某些噪声影响而造成模糊的图像进行复原。在对噪声作了某些统计性质的假定后,就可以用卡尔曼的算法以递推的方式从模糊图像中得到均方差最小的真实图像,使模糊的图像得到复原。  #PID算法 我们以小车作为参考点,重心受到一个额外的惯性力,与车轮加速度大小相同,方向相反。因此所受到的回复力为 F=mgsinα-macosα 根据控制系统的特征,角α需要控制在很小的范围内,并且假设控制车轮加速度与角α成正比,比例系数为k1,因此上式可近似处理为 F=mgα-mk1α 此时,只要k1>g,回复力的方向便和位移方向相反,此时小车可以恢复倒平衡位置。为使小车能在平衡位置尽快的稳定下来,还需要由阻尼力,阻尼力与角速度方向相反,大小成正比。 F=mgα-mk1-mk2α‘ 式中,k1,k2均为比例系数,α为小车小车倾角,α’为角速度,只要满足k1>g,k2>0,便可以将小车维持在直立状态。 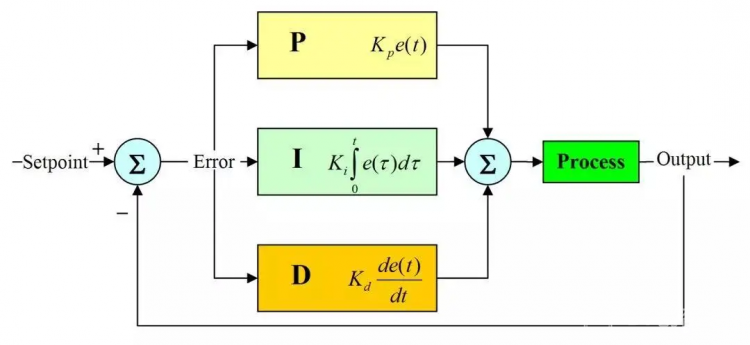 最后附上视频和程序,仅供大家参考,视频有点抖,主要本人太懒了,调PID太麻烦~~ |

44.63 KB, 下载次数: 3392
 沪公网安备31011502402448
沪公网安备31011502402448© 2013-2026 Comsenz Inc. Powered by Discuz! X3.4 Licensed