|
20045| 11
|
[进阶] 自制四轴飞行器飞控入门必读--如何理解和计算姿态角 |
|
最近又来研究研究有关飞行姿态解算的算法,看看当时没搞懂的四元数算法。主要也是学了网上几位大神的资源,才能小有所得。在这先附上参考一些大神心得的网址: https://zh.wikipedia.org/wiki/四元數 四元数维基百科 https://zh.wikipedia.org/wiki/向量 向量维基百科 【Unity技巧】四元数(Quaternion)和旋转 http://blog.csdn.net/candycat1992/article/details/41254799 学习笔记—四元数与欧拉角之间的转换 http://blog.csdn.net/candycat1992/article/details/41254799 [小应用]GD32F103+MPU9150 四轴飞行器第一步:9DOF姿态融合-GigaDevice GD32 MCU论坛 http://bbs.21ic.com/icview-605405-1-1.html 很多解释上面帖子里都有了。我想从另一个方向来写这篇文章。 先来说说我了解这个东西的经过吧。 说起对飞行姿态的解算,其实是相当复杂的一个过程,并不像我们一般认为的那么简单。首先,一开始(包括我自己)一般可能有个误区: 姿态不就一个倾角嘛(类比斜面)?所以感觉只需要求一个倾斜角而已,感觉挺简单的。仔细一想,发现其实有姿态有2个角度, 可以想象一个滑梯再像侧面翻滚一下,这样其实对于空间思维不太好的人已经有一点难度了。然后发现还需要再加一个是描述物体本身自旋的姿态。那么最后的结论为,姿态总共有3个轴。 那么以我本身的知识来说,如何能够检测出物体姿态的这3个变量呢? 总共需要3个传感器。 第一步:+加速度传感器。 说起测量倾斜角,一般能看见的都使用水泡,铅垂线之类的东西。有传感器使用经验的第一感觉就会觉得使用重力传感器就OK啦。 首先说说重力传感器的原理,这里说的重力传感器又叫加速度传感器。 加速度计和陀螺仪指南(很详细的介绍) http://blog.csdn.net/lovewubo/article/details/9084291 了解了这个东西以后,那么问题来了,仅仅靠加速度计能否完成角度的测量?答案是在静态情况下可以,在动态情况下不可以。 加速度传感器,从这个名字(以及上面的原理)也可以看出,其测不是重力,而是重力引起的类似加速度带来的效应。所以对于其他的加速度同样会有读数(运动状态的改变),特别在震动的时候(震动状态),该传感器会有非常大的数据变化,此时的数据难以反应重力的实际值,所以结论是单靠加速度传感器无法完成姿态解算。 第二步:+陀螺仪 既然单靠加速度传感器无法完成姿态解算,那还需要添加哪些传感器?通过上面资料 我们可以找到至少还需要的一个传感器,陀螺仪。 陀螺仪测量出的数据为绕各个轴的旋转角速度。 通过高等数学的知识可以得出,对角速度进行积分,可以得到旋转角度。把旋转角度加到之前测出的姿态上,会得到一个新的姿态,设为姿态A,通过加速度传感器可以算出来一个姿态B,这样将这两个姿态一定融合,就可以得到一个比较准确的姿态,这也就是之后我们可以进行姿态融合的基础。 第三步:+地磁场传感器 其实我们还缺一个传感器,地磁场传感器,其实他有个通俗的名字:电子罗盘。 说到这,可能有人就已经知道为什么需要这个传感器了。当加速度传感器完全水平的时候,可以预料,重力传感器无法分辨出在水平面旋转的角度即绕Z轴的旋转无法显示出来,此时只有陀螺仪可以检测。  于是又回到第一步时的问题。 陀螺仪虽然动态十分快速,但由于其工作原理是积分,所以在静态会有累计误差,表现为角度会一直增加或者一直减少。。 于是我们会需要一个在水平位置能确认朝向的传感器,这就是如今IMU(惯性导航单元)必备的第三个传感器,地磁场传感器,通过这3个传感器的相互校正,我们终于在大的理论上可以得到比较准确的姿态参数了。 总结一下前三步: 1、确定姿态我们需要三个轴上旋转的数据。 2、我们需要三个传感器,分别为3轴加速度传感器,3轴陀螺仪,以及3轴地磁场传感器。 完成这三步,可以说在大体姿态解算的框架上我已经有了概念,但具体怎么做还是两眼一抹黑啊。于是本着站在巨人的肩膀上做事的原则,我又开始漫长的资料搜索以及筛选。于是有了本文。 第四步 了解什么叫姿态 请各位自带笔和纸,复习或者预习大学高等数学,线性代数,复变函数,等数学知识,听我慢慢回忆的学习的过程。。。 既然我一直说姿态解算,姿态解算,那到底什么是姿态。 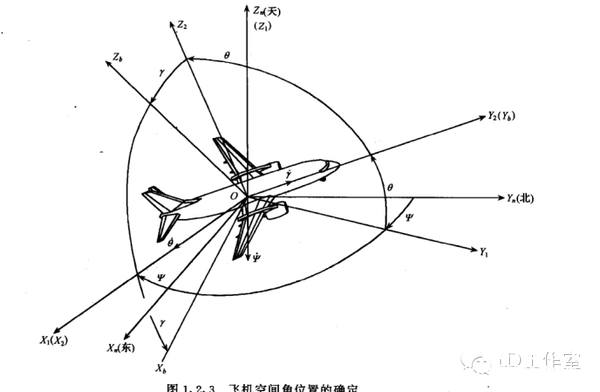 上图,我们想象一个飞机在天空飞行,他可能侧倾,可能仰俯,也可能旋转,这就是我们平时所说的姿态,那么这个姿态抽象出来意味着什么呢?这里是重点啦: 姿态,就是一个坐标系与另一个坐标系的转换关系。 这个可能比较抽象哈。 首先在飞机上建立一个坐标系,X轴为机翼的方向,Y轴为机头的方向,Z轴垂直于飞机,这个坐标系是随着飞机姿态改变而变动的,此时就要求飞机的姿态,就等价于求出这个坐标系,那么如何得到这个坐标系?要得到一个新的坐标系,首先要有一个参考坐标系,一般选取Y轴正向为正北,x正向为正东,z轴垂直于地平面了,给他取个名字,就叫地理坐标系吧。 所以此时,我们所说的姿态其实就是飞机坐标系和地理坐标系(是固定的)的一种关系。 现在我们终于可以进入第五步啦。 第五步: 如何表示这种关系。找到了表示这种关系的方法,就可以利用这个方法随意转换这2个坐标系。先上结论吧。 有三种关系表示方式: 1、欧拉角 2、余弦矩阵 3、四元数 1、欧拉角 欧拉角是很直观的,一个物体的旋转,可以分解到三个坐标轴上的旋转。这三个旋转角度就是欧拉角。 在惯性系统中一般把这三个角度分别称为roll,pitch,yaw。上个直观的图,很容易理解。 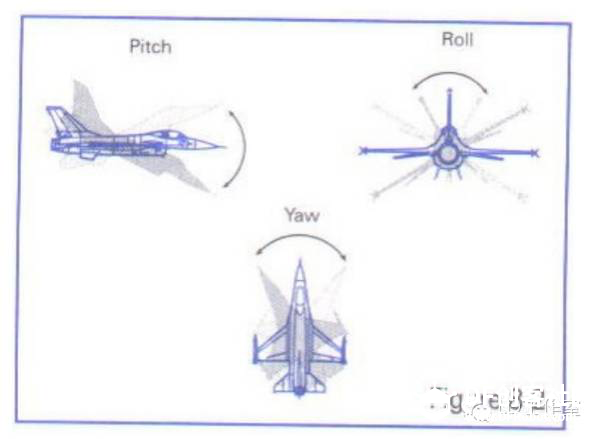 用欧拉角来描述物体的旋转不光需要有角度,还需要有旋转顺序,一般旋转顺序是先yaw后pitch,再roll反应到坐标轴上就是先绕Z轴旋转,再绕X轴旋转,最后绕Y轴旋转。为什么有顺序呢?是否可以没顺序?如果身边有东西可以转转看,这个问题之后在理论上会进行说明。 需要注意的是 yaw pitch roll 都是对应的固定的参考系 也就是上面说的地理坐标系而言,每次新的姿态坐标系都是由地理坐标系通过欧拉角旋转得到的。 这样我们就用欧拉角表示了物体的姿态。 欧拉角是有很多优点的。但是也有致命的缺点,那就是 Gimbal Lock(万向节死锁) ,要 理解 Gimbal Lock所说的情况(可能有点难)让我们看个现实中的场景。 假如我们有一个望远镜和一个用来放望远镜的三脚架, (我们将)三脚架放在地面上, 使支撑望远镜的三脚架的顶部是平行于地平面(参考平面)的,以便使得竖向的旋转轴(记 为 x 轴)是完全地垂直于地平面的。现在,我们就可以将望远镜饶 x 轴旋转 360度,从而观 察 (以望远镜为中心的) 水平包围圈的所有方向。 通常将正北朝向方位角度记为 0 度方位角。 第二个坐标轴,即平行于地平面的横向的坐标轴(记为y 轴)使得望远镜可以饶着它上下旋转,通常将地平面朝向的仰角记为 0 度,这样,望远镜可以向上仰+90 度指向天顶,或者向 下-90 度指向脚底。好了,万事俱备。现在,天空中(包括地面上)的每个点只需要唯一的 一对 x 和 y 度数就可以确定。比如 x=90 度,y=45 度指向的点是位于正东方向的半天空上。 现在,看看万向节死锁是怎么发生的。一次,我们探测到有一个飞行器贴地飞行,位于望远 镜的正东方向(x=90 度,y=10 度) ,朝着我们直飞过来,我们跟踪它。飞行器飞行方向是 保持 x 轴角度 90 度不变,而 y 向的角度在慢慢增大。随着飞行器的临近,y 轴角增长的越 来越快且当 y向的角度达到 90 度时(即将超越) ,突然它急转弯朝南飞去。这时,我们发现 我们不能将望远镜朝向南方(在只绕一个轴旋转的情况下),因为此时 y向已经是 90度!造成我们失去跟踪目标。这就是 万向节死锁! 为什么说不能将望远镜朝向南方呢,让我们看看坐标变化,从开始的(x=90度,y=10 度)到(x=90 度,y=90 度) ,这个过程没有问题,望远镜慢慢转动跟踪飞行器。当飞行器 到达(x=90 度,y=90 度)后,坐标突然变成(x=180 度,y=90 度) (因为朝南) ,x 由 90 突变成 180 度,所以望远镜需要饶垂直轴向 x 轴旋转 180-90=90 度以便追上飞行器,但此时, 望远镜已经是平行于 x 轴,我们知道饶平行于自身的中轴线的的旋转改变不了朝向,就象拧 螺丝一样,螺丝头的指向不变。所以望远镜的指向还是天顶。而后由于飞行器飞远,坐标变 成(x=180 度,y<90 度)时,y 向角减小,望远镜只能又转回到正东指向,望'器'兴叹。 这 说明用 x,y旋转角(又称欧拉角)来定向物体有时并不能按照你想像的那样工作,象上面的 例子中从(x=90度,y=10度)到(x=90 度,y=90度) ,按照欧拉角旋转确实可以正确地定 向,但从(x=90度,y=90度)到(x=180 度,y=90 度) ,再到(x=180度,y<90 度),按照 欧拉角旋转后的定向并非正确。我的理解是坐标值的变化和飞行器空间的位置变化一一对 应,但是从(x=90 度,y=90 度)到(x=180 度,y=90 度) ,再到(x=180 度,y<90 度)这个变化,飞行器位置是连续的变化,但坐标值的变化却不是连续的(从 90 突变到 180) ,其原因在于(x=90 度,y=90 度)和(x=180 度,y=90 度)甚至和(x=任意 度,y=90 度)这些不同的坐标值对应空间同一个位置,这种多个坐标值对应同一个位置的 不一致性是造成死锁的根源。 上面是 2 维坐标系中的例子, 同样, 对于 3 维的也一样。 比如有一个平行于 x 轴的向量, 我们先将它饶 y旋转直到它平行于 z 轴,这时,我们会发现任何饶 z的旋转都改变不了向量 的方向,即万向节死锁,所以说传统的欧拉角是不能做到全姿态解析的。 2.方向余弦矩阵。 说方向余弦矩阵之前,先讨论方向余弦。 一个向量的方向(姿态)我们可以用他在参考坐标系(地理坐标系)各个轴向的夹角的余弦来表示(及在各个轴的投影)。 类似的 一个坐标系 可以看成是3个向量组成,所以三个向量分别在坐标轴上的投影可以用来表示一个坐标系与参考坐标系的关系。这总共9个方向余弦组成了一个三阶矩阵,其对应方式如下图。 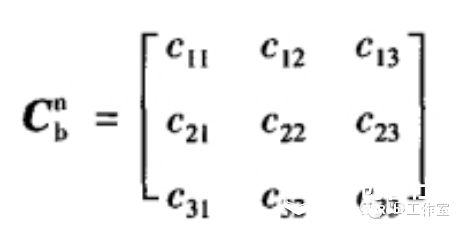 第 i 行、 j 列的元素表示参考坐标系 i 轴和姿态坐标系 j 轴夹角的余弦。 事实上 方向余弦和欧拉角没有本质区别,因为方向余弦实际上就是用欧拉角表示的。 下面附上推倒具体表达式的方法 先从二维坐标系转换开始。 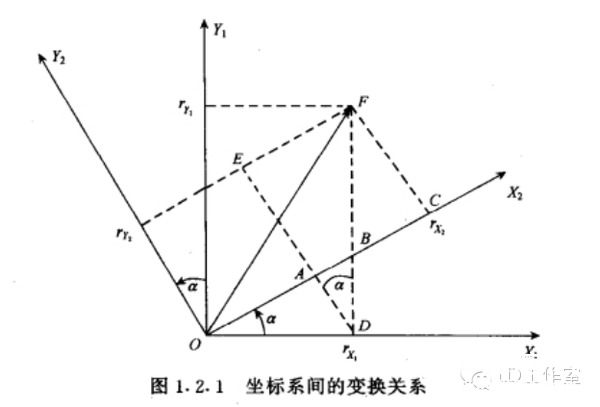 推广到三轴的单次旋转,我们用矩阵表示为(绕Z轴旋转): 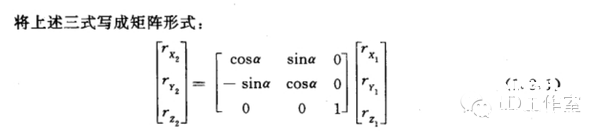 这里要说一下矩阵的含义,C2 1表示坐标系 1 到坐标系 2 的变换矩阵,那么有 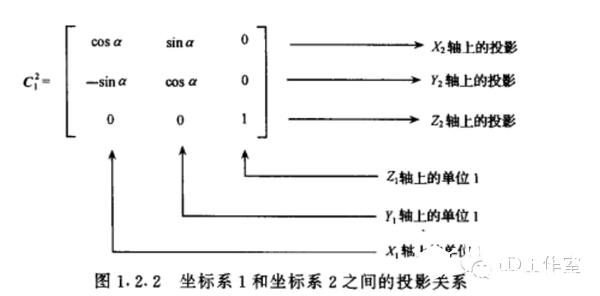 这样我们可以得到3个变换矩阵 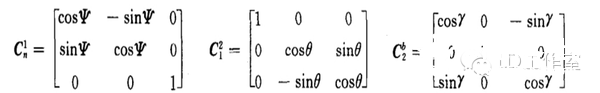 分别为单独绕Z轴旋转,绕X轴旋转,绕Y轴旋转。 实际上,两坐标系任何复杂的角位置关系都可以看做有限次基本旋转的组合,变换矩阵 等于基本旋转确定的变换矩阵的连乘(线性代数), 连 乘的基本顺序依据基本旋转的顺序向右排列。 之所以有顺序是因为矩阵有“左乘”和“右乘” 之分(还是线性代数)。那么我们得到: 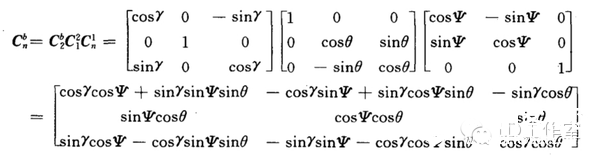 最后的矩阵就是完整的余弦矩阵。γ、θ、ψ就是欧拉角啦。 至此我们解释了为什么欧拉角会有旋转的顺序之分。从以上数学计算可以看出不同的旋转次序会带来不同的结果。 四元数: 四元数要介绍的太多了。。因为他优点有很多,利用起来也很方便,但是理解起来太抽象了。 百度四元数,一开始看到的就是四元数来历,还有就是四元数的基本计算。 对于 来历,还是想说一下,四元数(Quaternions)是由威廉·卢云·哈密尔顿(William Rowan Hamilton,1805-1865)在 1843 年爱尔兰发现的数学概念(百度百科)。 将实数域扩充到复数域,并用复数来表示平面向量,用复数的加、乘运算表示平面向量 的合成、伸缩和旋,这就是我们熟知的复数的二维空间含义,所以人们会继续猜想,利用三 维复数不就可以表达三维空间的变换了吗,历史上有很多数学家试图寻找过三维的复数, 但 后来证明这样的三维复数是不存在的。 有关这个结论的证明,我没有查到更明确的版本, 据 《古今数学思想》中的一个理由,三维空间中的伸缩旋转变换需要四个变量来决定:两个变 量决定轴的方向,一个变量决定旋转角度,一个变量决定伸缩比例。这样,只有三个变量的 三维复数无法满足这样的要求。但是历史上得到的应该是比这个更强的结论,即使不考虑空 间旋转,只从代数角度来说,三维的复数域作为普通复数域的扩张域是不存在的。 并且, 据 《古今数学思想》叙述,即使像哈密尔顿后来引入四元数那样,牺牲乘法交换律,这样的三 维复数也得不到。经过一些年的努力之后, Hamilton 发现自己被迫应作两个让步,第一个 是他的新数包含四个分量,而第二个是他必须牺牲乘法交换律。 ( 《古今数学思想》第三册 177 页 )但是四元数用作旋转的作用明显,简化了运算,而且避免了 Gimbal Lock。 四元数 是最简单的超复数,我们不能把四元数简单的理解为 3D 空间的矢量,它是 4 维空间中的 的矢量,也是非常不容易想像的。 那什么是四元数呢? 在维基百科中截取一段: 复数是由实数加上虚数单位 i 组成,其中  相似地,四元数都是由实数加上三个元素 i、j、k 组成,而且它们有如下的关系:  每个四元数都是 1、i、j 和 k 的线性组合,即是四元数一般可表示为  要把两个四元数相加只需将同类的系数加起来就可以,就像复数一样。 那么四元数如何表示旋转呢? 再截取维基百科上的一段话 群旋转 主条目:四元数与空间旋转 非零四元数的乘法群在R3的实部为零的部分上的共轭作用可以实现转动。单位四元数(绝对值为1的四元数)若实部为cos(t),它的共轭作用是一个角度为2t的转动,转轴为虚部的方向。 提取几个关键词: 四元数表示转动,首先其模应该为1,如下  这个值应该为1。 此时实部,也就是a若等于cos(t)则他的共轭作用为一个2t的转动,转轴方向为向量(b,c,d)的方向。 那什么叫共轭作用?实际上就是四元数表示旋转的方式。 那么利用四元数代表旋转是如何实现的,在载体系定义的一个矢量 r b 可以直接 利用四元数将其在参考系中表示为 rn 。首先定义一个四元数 rb' ,它的虚部等于 rb的相应分量,标量分量为零: 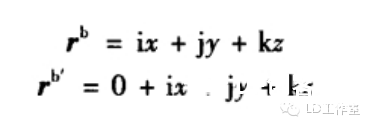 参考系中的 r n’ 表示为 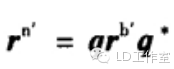 这也就是共轭作用。 ,其中 q = a + bi + cj +dk,q* 为q复共轭,q = a - bi - cj -dk及因此有: 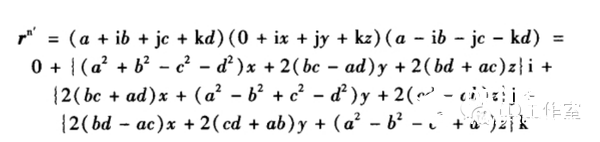 写成矩阵式: 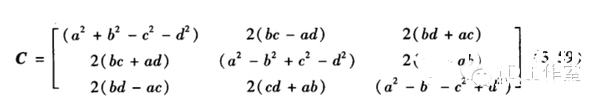 因为都表示旋转,所以这个矩阵理论上应该和余弦矩阵是等效的,从而就能计算欧拉角了。 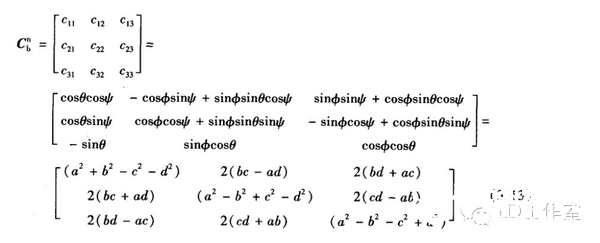 上图显示了四元数和余弦矩阵的关系。 这样反求出欧拉角如下图: 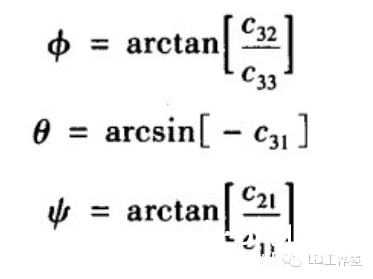 此时就可以根据四元数反求出欧拉角了。 |
 活跃会员
活跃会员
 沪公网安备31011502402448
沪公网安备31011502402448© 2013-2026 Comsenz Inc. Powered by Discuz! X3.4 Licensed