|
14794| 11
|
[项目分享] 圆周率计算器v3.0终极版(不再更新) |
|
本帖最后由 爱bc的小学生 于 2023-1-11 14:11 编辑 上次的圆周率v2.0有太多bug,这次只保留以前的线程2,直接重做。还参考了一些scratch进阶书籍旧版链接:圆周率计算器 - DF创客社区 - 分享创造的喜悦 (dfrobot.com.cn) 圆周率v3.0(Mind+)使用积木块658 1.新增6种计算方法 2.废除以前的低效率网传计算方法 3.角色在割圆法展示版中说的“只和实际查了xxxxxx”这个xxxxxx出现了负值,现在添加了“绝对值“xxxxxx””。 使用方法:和以前一样 1.点击小绿旗 2.根据说明输入计算方法对应的数字 3.开始精彩计算 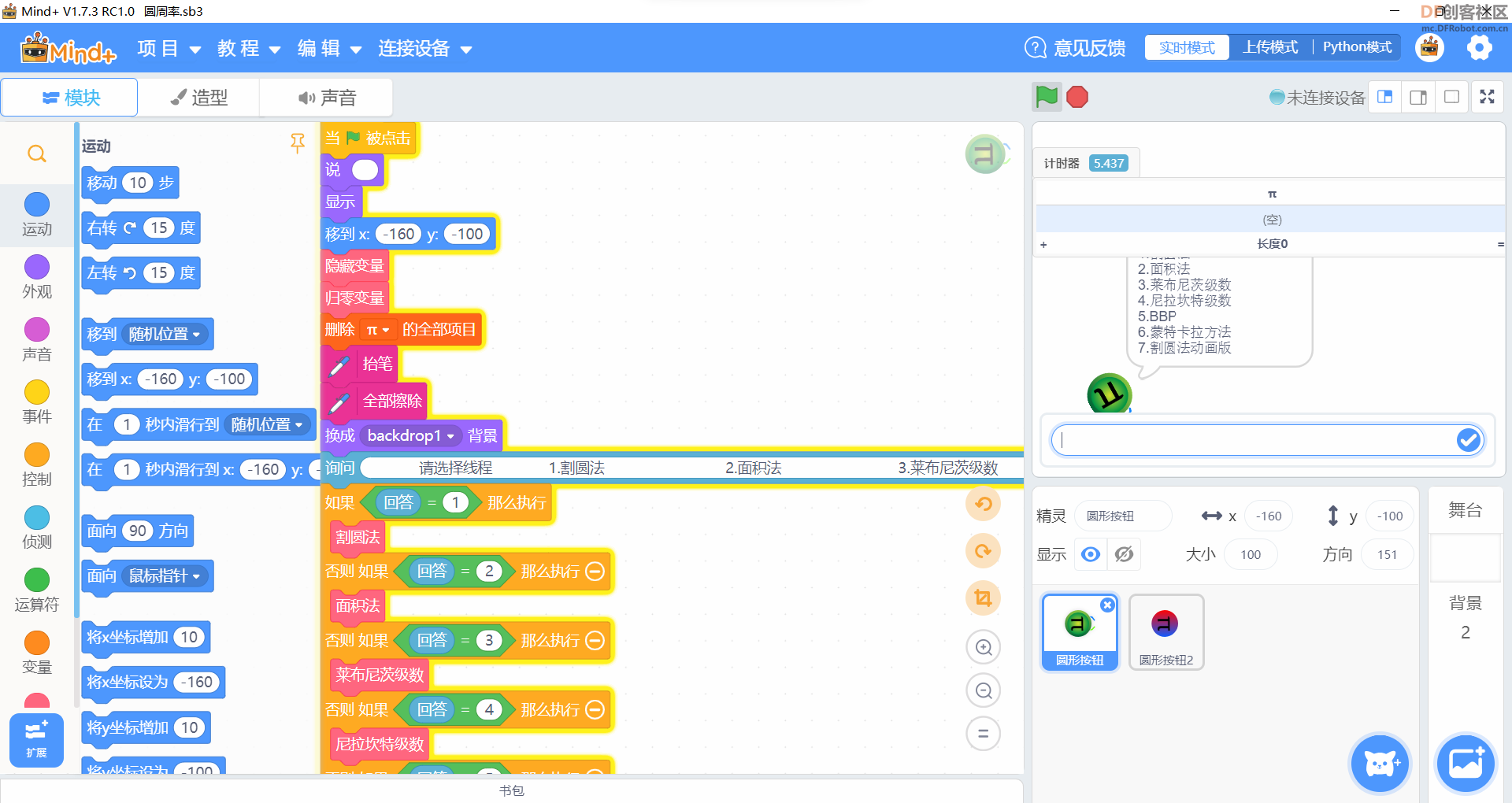 着急的网友们,点击这里先下载Mind+附件  圆周率.sb3.rar(将文件后缀名.rar删除即可用mind+打开) 圆周率.sb3.rar(将文件后缀名.rar删除即可用mind+打开)下面详细介绍算法:-------------------------------------------------------- Around1.割圆法 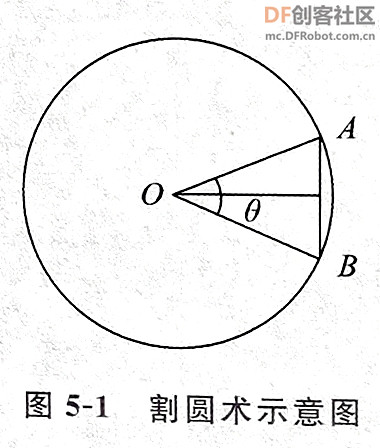  根据这个公式,只要不断增加 n 值,就能计算出越来越精确的圆周率。 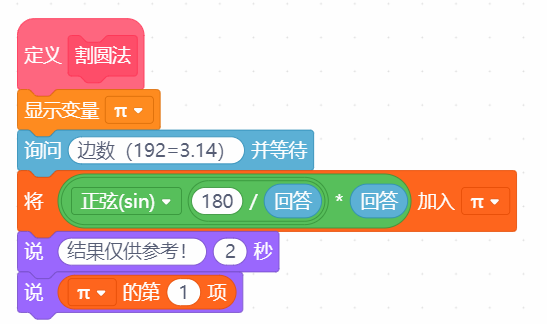 Around2.面积法 所谓"面积法",就是把圆等分,求正多边形的面积,分的份数越多,正多边形的面积就越接近圆的面积。 把一个圆等分为 n 份得到一个正 n 边形,那么圆心角0对应的弦长就等于正 n 边形的边长 d 。而圆心角0的两条边(圆的半径 r )与弦长(边长 d )构成一个三角形△ AOB ,所以正 n 边形的面积就等于 n 个三角形的面积之和,最后再用圆的面积公式计算圆周率。 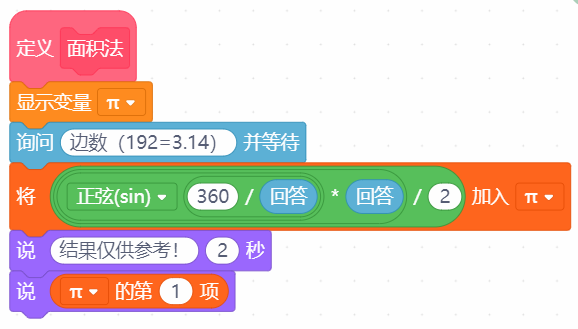 Around3.莱布尼茨级数 除了使用"割圆术"计算圆周率之外,数学家发现了若干个数学级数,如果进行无穷多次运算,就能精确计算出小数点后面的多位数字。有的无穷级数非常复杂,需要超级计算机才能运算处理;而有的则比较简单,如莱布尼茨级数和尼拉坎特哈级数。莱布尼茨级数又被称为格雷戈里.莱布尼茨级数,用以纪念与莱布尼茨同时代的天文学家兼数学家詹姆斯.格雷戈里。格雷戈里.莱布尼茨级数的结构非常简单,但是它的计算非常耗费时间,每一次迭代的结果都会缓慢地接近 x 的精确值。该级数的展开公式如下: 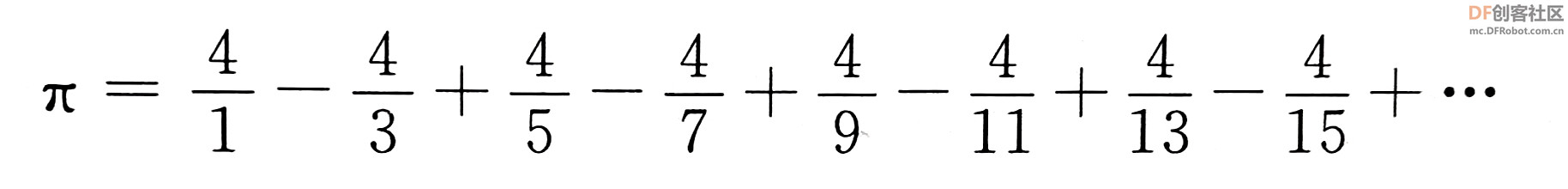 该公式的计算是依次交替进行减法和加法运算,参与运算的分数由分子为4、分母为连续的奇数构成。这个级数的收敛非常慢,需要进行非常多次的计算,才能使结果接近 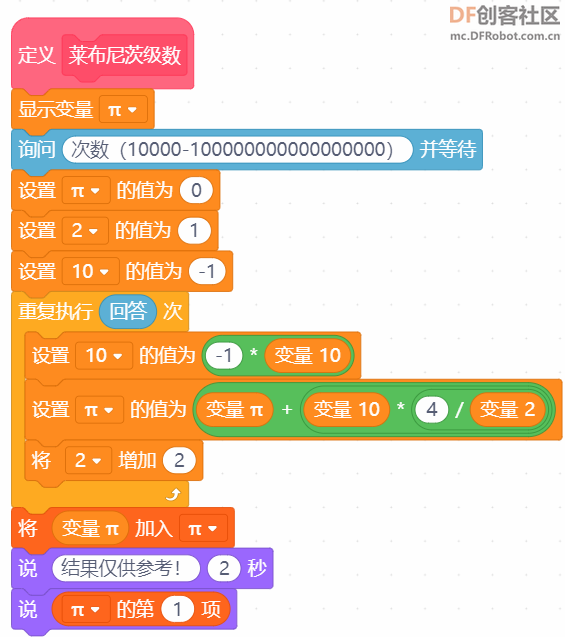 Around4.尼拉坎特级数 尼拉坎特哈级数是印度数学家尼拉坎特哈发现的一个可用于计算元的无穷级数。虽然它的结构比莱布尼茨公式复杂一些,但是它的收敛速度快,能够比莱布尼茨公式更快地接近 。该级数的展开公式如下: 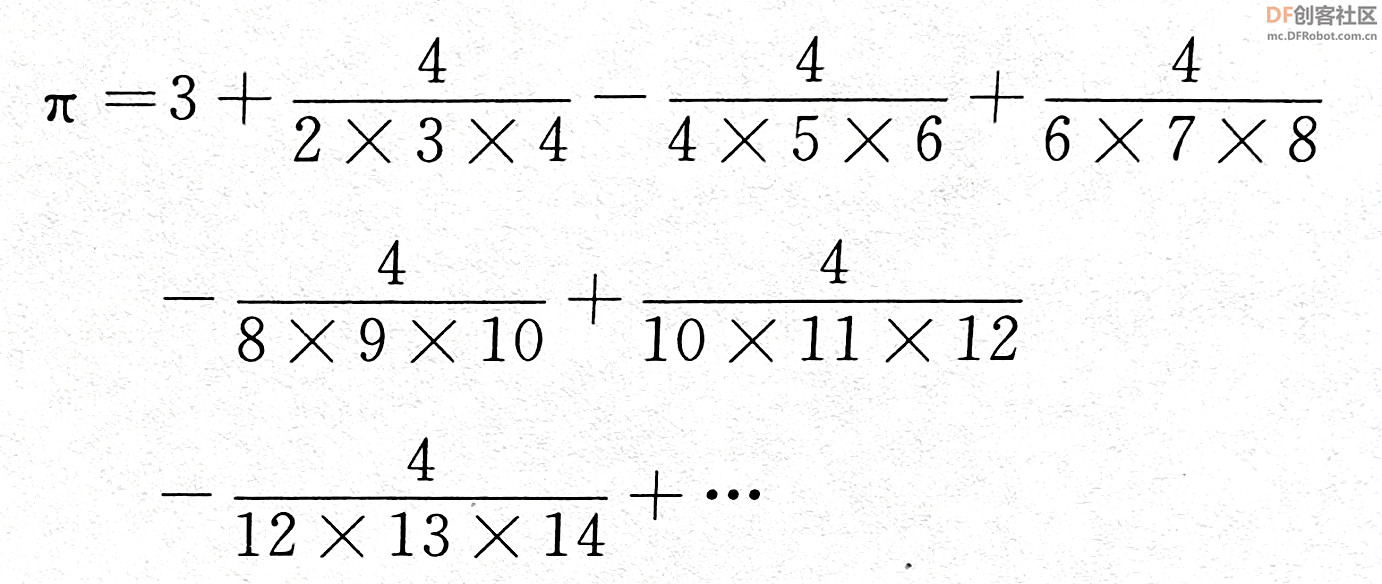 该公式的计算从3开始,依次交替进行加法和减法运算,参与运算的分数由分子为4、分母为三个连续整数乘积构成。在每次迭代时,三个连续整数中的最小整数是上次迭代时三个整数中的最大整数。这个级数的收敛比较快,反复计算若干次,结果就非常后接近。 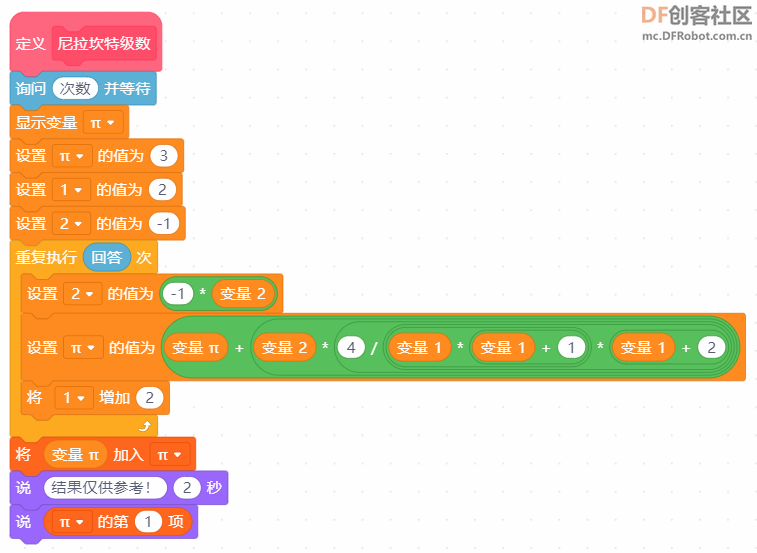 Around5.BBP BBP 公式全称为贝利﹣波尔温﹣普劳夫公式( Bailey - Borwein - Plouffeformula ),由 DavidBailey 、 PeterBorwein 和 SimonPlouffe 于1995年共同发表,以三位发表者的名字命名。该公式如下: 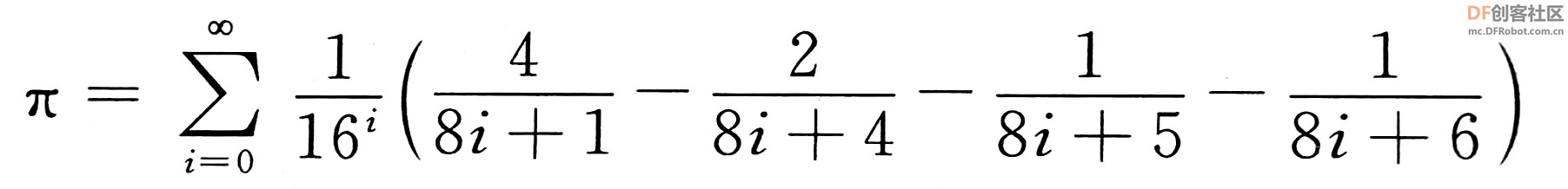 传统圆周率计算需要计算其前 n 位,这需要巨大的空间消耗,而 BBP 公式能直接从指定位置开始计算,不需要巨大的内存和计算能力。该公式打破了传统圆周率的算法,可以计算圆周率的任意第 n 位,而不需计算前面的 n -1位。这为圆周率的分布式计算提供了可行性。 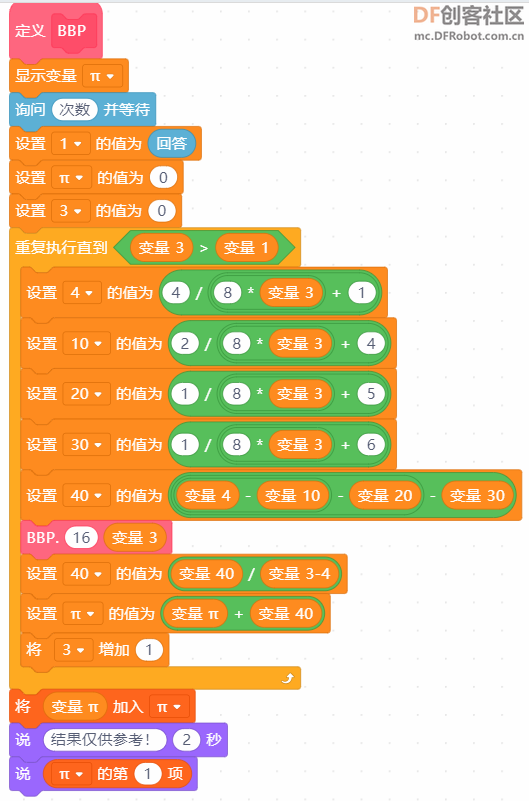 Around6.蒙特卡拉方法(不准确) 蒙特卡罗方法又称统计模拟法,是一种随机模拟方法。它以概率和统计理论方法为生行求和;每值 pi 输出。公式中括号基础,使用随机数(或更常见的伪随机数)来解决许多计算问题。 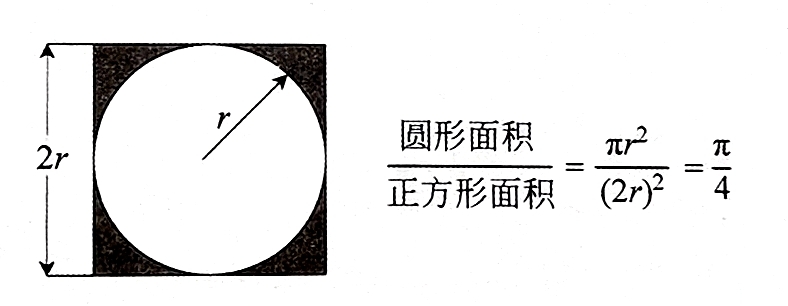 计算两点间距离公式为 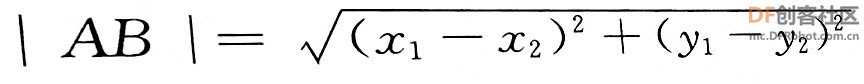 取目标点 ,所以公式简化为 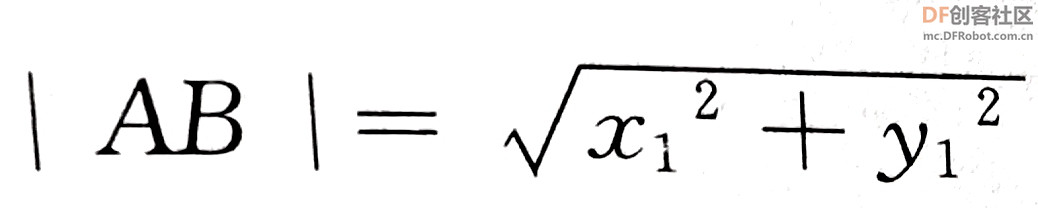 如果这些随机产生的点均匀分布,那么圆内的点应该占到所有点的π /4,因此将这个比值乘以4,就是π的值。 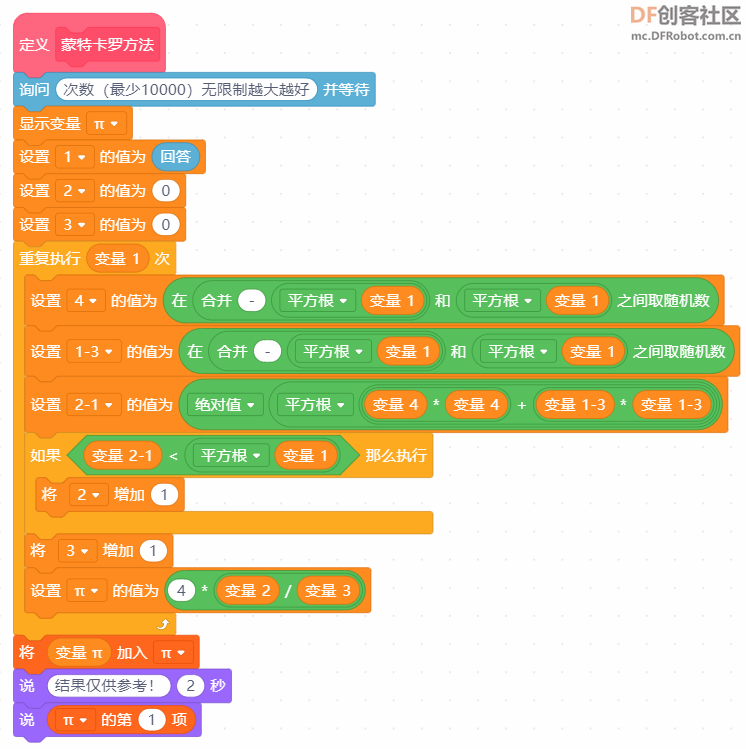 |
 沪公网安备31011502402448
沪公网安备31011502402448© 2013-2026 Comsenz Inc. Powered by Discuz! X3.4 Licensed