使用DFR1188实现简单的pid控制实例

经历了上一次的简单入门体验（Firework！BOOM!（基于DFR1188简单的烟花生成））
接下来我们可以try一下进阶的项目了，比如接下来我将会展示一个简单的PID控制实例。
本次依然使用DFR1188开发板，得益于RP2350的强大性能，比普通用途更精密、更复杂、更高速的控制算法也可以完成。
环境配置方面可以看看我上面↑之前的帖子或参考社区其它相关内容，这里就不过多赘述了。
一、项目介绍
本次项目的灵感源自于曾经电脑装机多剩出来一个机箱风扇（12V,0.19A），突然想到现在的机箱风扇都是PWM调速，既然可以调速，那么操作空间就大了。

最开始我想制作一个基于温度自动调速的风扇，但是感觉太没创意了，而且我也没有一个能让我便捷测试效果的热源。后来看到之前买的角度传感器（MPU6050）有了一个新点子......
如图这是一块普通的硬纸板，现在先固定上角度传感器。

再把它和风扇一起固定到架子上（其实这个小龙门架是我做激光雕刻的残次品，没想到有一天还能派上用场）就构成了完整结构

接下来的目标是：通过风扇吹起纸板使之角度固定在一个设定值，风扇的转速控制使用pid算法，控制逻辑闭环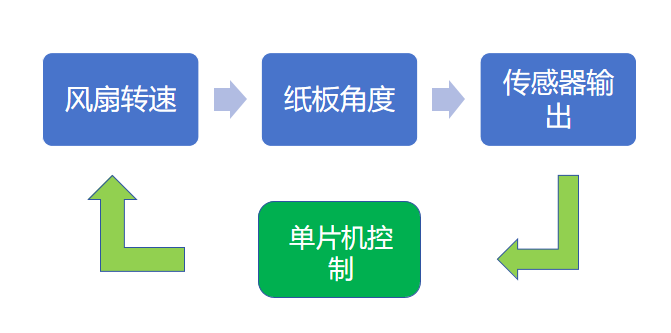

二、控制原理
PID控制如雷贯耳，从我刚上大学时就有所耳闻，没接触之前一直认为它是一个非常高端的专业名词，但是实际使用上之后才发现原理原来真的不是很难，难的只是调参过程（何止是难，简直是太痛苦了）
简而言之，PID分为三个部分：比例（Proportional）、积分（Integral）、微分（Derivative），PID这个名字正是取其首字母。

1. 比例控制（P）
如果你去搜索什么是比例控制，百度会回复你“依据输出与当前误差（设定值与实际值之差）的比例进行控制”，这句话看起来还是很抽象的，不妨来看一个例子。小学时大家一定做过一个经典题目，泳池一边放水一边注水，多久能把水池填满？通常注水和放水的速度是固定的，但是在现实世界中很多的控制是，我们需要依据泳池里的剩余水量来改变注水的速度，举例一个量化的情况：有一个泳池，控制目标是要保证泳池的水位保持在1米的高度。t=0时，水池里的水位是0.2米，那么当前时刻的水位和目标水位之间是存在一个误差的e，且e为0.8.这时，管理员通过加水的方式来控制水位。如果单纯的用比例控制算法，就是指加入的水量u和误差e是成正比的。即
u=kp*error
假设kp取0.5，那么t=1时（表示第1次加水，也就是第一次对系统施加控制），那么u=0.5*0.8=0.4，所以这一次加入的水量会使水位在0.2的基础上上升0.4，达到0.6.
接着，t=2时刻（第2次施加控制），当前水位是0.6，所以error是0.4。u=0.5*0.4=0.2，会使水位再次上升0.2，达到0.8.
如此这么循环下去，就是比例控制算法的运行方法。
可以看到，最终水位会达到我们需要的1米。
但是，考虑另外一种情况，在加水的过程中，存在漏水的情况，假设每次在加水的时间中，都会漏掉0.1米高度的水。仍然假设kp取0.5，那么会存在着某种情况，假设经过几次加水，水位到0.8时，将不会再变换！因为，水位为0.8，则误差e=0.2. 所以每次加水的量为u=0.5*0.2=0.1.同时，每次加水，又会流出去0.1米的水，加入的水和流出的水相抵消，水位将不再变化！
也就是说，我的目标是1米，但是最后系统达到0.8米的水位就不再变化了，且系统已经达到稳定。由此产生的误差就是稳态误差了。

如何处理稳态误差？就要用到接下来的部分了。

2. 积分控制（I）
在上面的例子中，如果仅使用比例控制，会存在稳态误差，最后的水位就卡在0.8了。于是，在控制中，再引入一个分量，对注水量u进行一个修正，该分量和误差的积分是正比关系。所以，比例+积分控制算法为：
u=kp*e+ ki∗∫ e
还是用上面的例子，第一次的误差e是0.8，第二次的误差是0.4，至此，误差的积分（此时是离散情况，积分其实就是做累加），∫e=0.8+0.4=1.2. 这个时候的控制量，除了比例的那一部分，还有一部分就是一个系数ki乘以这个积分项。由于这个积分项会将前面若干次的误差进行累计，所以可以很好的消除稳态误差（假设在仅有比例项的情况下，系统卡在稳态误差了，即上例中的0.8，由于加入了积分项的存在，会让输入增大，从而使得水缸的水位可以大于0.8，渐渐到达目标的1.0.）这就是积分项的作用。
但是我们又发现了一个新的问题：由于积分项的存在，注水量增大后可能将会超出我们的设定目标值，然后u在减小后又会低于目标值，会始终造成震荡，无法稳定维持在我们的目标值上，这又该怎么解决呢？

3. 微分控制（D）
于是我们引入了微分控制。微分，说白了在离散情况下，就是e的差值，就是t时刻和t-1时刻e的差，即u=kd*（e（t）-e（t-1））
换一个例子：汽车定速巡航时，如果只用比例控制，车速容易因惯性超过目标值再回调，形成反复加速减速的顿挫感。微分控制的作用就是监测车速变化趋势——当检测到车速正在快速接近目标时（比如从90km/h加速到95km/h），它会自动减小油门，相当于"提前轻踩刹车"，防止车速冲过头。就像骑自行车下坡时，看到坡道变缓会提前捏闸减速一样，D控制让系统平稳接近目标，避免震荡。这种"预见性调节"在无人机平衡、机器人控制中同样有所应用，能有效抑制超调，使运动更顺滑。


把上述结合起来，我们就得到了最终的控制公式：（以下公式图片来自于知乎）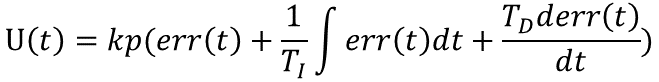

括号内第一项是比例项，第二项是积分项，第三项是微分项，前面仅仅是一个系数。很多情况下，仅仅需要在离散的时候使用，则控制可以化为：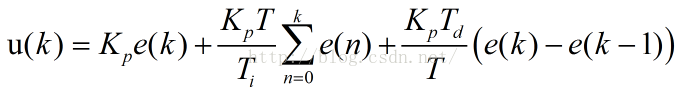

每一项前面都有系数，这些系数都是需要实验中去尝试然后确定的，为了方便起见，将这些系数进行统一一下：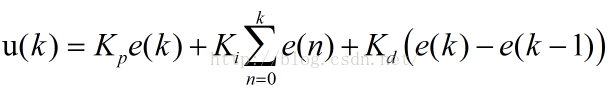

这里的Kp，Ki，Kd就是我们pid控制中需要调试的参数了。
三、代码实现
接下来先展示一下实际效果，由于控制效果看起来不明显，我加入了一个小LED，这个LED的亮度与控制量的绝对值abs（u(k)）呈正相关，用于展示控制作用量的作用强度。

（↑无外力作用）

（↑施加外力偏移目标值）

（↑施加更大的外力）
可以看到这三次黄色LED的亮度是越来越亮的，代表PID控制的作用强度越来越高（其实即使在无外力作用时，因为参数调节的不精确和其他因素影响，控制精度达不到很高，LED始终在低亮度范围微微闪烁，图1是我捕捉到亮度最暗的时刻了。。。）
代码展示：

#include <Wire.h>

const int MPU_ADDR = 0x68; //mpu6050的I2C地址
int16_t ax, ay, az;
const int ledPin = 8;
const int PWM_fan = 9;
int pwm1 = 0; //pwm控制的模拟值
float w = 0.0; //俯仰角

//pid参数
float Kp = 10.0;
float Ki = 1.1;
float Kd = 4.5;

float rf = -75.0;  //目标角度
float error, lastError = 0, integral = 0;
unsigned long lastTime = 0;

float MPU6050data(){
  // 读取6050的数据
  Wire.beginTransmission(MPU_ADDR);
  Wire.write(0x3B); 
  Wire.endTransmission(false);
  Wire.requestFrom(MPU_ADDR, 6, true); 
  ax = Wire.read() << 8 | Wire.read();
  ay = Wire.read() << 8 | Wire.read();
  az = Wire.read() << 8 | Wire.read();

  // 角度
  float axf = ax / 16384.0;
  float ayf = ay / 16384.0;
  float azf = az / 16384.0;
  float pitch = atan2(axf, sqrt(ayf * ayf + azf * azf)) * 180 / PI;
  float roll  = atan2(ayf, sqrt(axf * axf + azf * azf)) * 180 / PI;
  return pitch ;
  // Serial.print("Pitch: ");
  // Serial.print(pitch);
  // Serial.print(" | Roll: ");
  // Serial.println(roll);
  // delay(200);
}
void pid(float pitch,int fanPin){
  unsigned long now = millis();
  float dt = (now - lastTime) / 1000.0;
  lastTime = now;
  // pid 控制
  error = rf - pitch;
  integral += error * dt;
  float derivative = (error - lastError) / dt;
  float output = Kp * error + Ki * integral + Kd * derivative;
  lastError = error;
  output = constrain(output, 0, 255);
  analogWrite(fanPin, (int)output);
  delay(20); 
}

void ledview(float data){
  w = data;
  if (abs((w-rf)/15*255>255)){
    pwm1 = 255;
  }
  else{
    pwm1 = int(abs((w-rf)/15*255));
  }
  analogWrite(ledPin, pwm1);
}

void setup() {
  Wire.begin();
  Serial.begin(115200);
  //初始化6050
  Wire.beginTransmission(MPU_ADDR);
  Wire.write(0x6B); 
  Wire.write(0); 
  Wire.endTransmission(true);
  pinMode(ledPin, OUTPUT);
  pinMode(PWM_fan, OUTPUT);
}

void loop() {
  ledview(MPU6050data());
  pid(w,PWM_fan);
}
复制代码

注意，对于一个pid控制实例想要复现的话是很难的，因为其原理虽然是相同的，但是受其他各种因素的影响参数不可能一样的，我这个参数也只是简单调试了一下，并没有达到最优的地步，但是pid调参成功真的是很有成就感的，各位可以自己也去试试。
后面可能会尝试一下实现MPC控制，敬请期待