本帖最后由 iooops 于 2016-3-31 20:47 编辑
Yeap!!第二天~~好像有点晚 - - 下次早上发。
【说明】
Fibonacci为1200年代的欧洲数学家,在他的着作中曾经提到:若有一只兔子每个月生一只小兔子,一个月后小兔子也开始生产。起初只有一只大兔子,一个月后就有两只兔子(1大1小),二个月后有三只兔子(2大1小),三个月后有五只兔子(3大2小,小兔子投入生产)......。问第30个月能生多少只小兔子?(第0个月为0只小兔子起算)
先在草稿纸上画张兔子图推算看看哦。
注意新生的小免子需一个月成长期才会投入生产。
不知道你有没有画成下面这样 - -

呀 - - 好像有点糊 - -
【解法】
根据以上的数字:0、1、1 、2、3、5、8……我们可以总结出以下规律:
fn = 0 n = 0, 1
fn = fn-1 + fn-2 n ≥ 2
其中n代表月份,f代表当月能生产的小兔子数量。
上述的公式所代表的就是传说中的Fibonacci数列,一般习惯称之为费氏数列,例如以下: 0、1、1 、2、3、5、8、13、21、34、55、89......
但是我们发现,就算知道规律计算起来也比较麻烦有木有!!所以我们就可以用C语言来解决这个问题啦。
如下所示:
- #include <stdio.h>
- #include <stdlib.h>
-
- int fib(int n) {
- int Fib[n];
- int i;
- if(n > 0) {
- Fib[0] = 0;
- Fib[1] = 1;
- for(i = 2; i <= n; i++) {
- Fib[i] = Fib[i-1] + Fib[i-2];
- }
- for(i = 0; i <= n; i++){
- printf("%d ", Fib[i]);
- }
- printf("\n");
- printf("第%d个月能生产%d只兔子\n", n, Fib[n]);
- return 0;
- }
- else {
- return -1;
- }
- }
-
-
- int main(void) {
- int n;
- printf("请输入月数:");
- scanf("%d", &n);
- fib(n);
- return 0;
- }
论递归的重要性。
但是,当n变得越来越大的时候,O(n)的递归会变得越来越慢。为什么?这要从递归的核心开始说起……(自己查资料了解去)
其实,楼主在维基百科上还找到了其他解法,比如初等代数求解、线性代数求解以及组合法求解。其实……楼主只看得懂初等代数求解……
以下选自维基百科https://zh.wikipedia.org/wiki/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97
初等代数解法已知
首先构建等比数列设
化简得

比较系数可得:

不妨设 0, \alpha>0" class="mwe-math-fallback-image-inline tex"> 0, \alpha>0" class="mwe-math-fallback-image-inline tex">
解得:

所以有 , 即 , 即 为等比数列。 为等比数列。
求出数列{ }由以上可得: }由以上可得:

变形得: 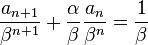 。 令 。 令
求数列{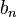 }进而得到{ }进而得到{ } }
设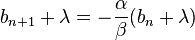 ,解得 ,解得 。 故数列 。 故数列 为等比数列 为等比数列
即 。而 。而 , 故有 , 故有
又有 和 和
可得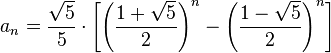
得出 表达式 表达式
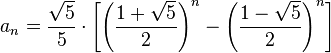
应用这种方法就不用那么大的递归开销了~~
C语言的实现如下:
- #include <stdio.h>
- #include <stdlib.h>
-
-
- int fib(int n)
- {
- double constant_a = (1 + sqrt(5)) / 2;
- double constant_b = (1 - sqrt(5)) / 2;
- double constant_c = sqrt(5) / 5;
- double value_1 = 0;
- int value_2 = 0;
- if(n > 0)
- {
- for (int i = 0; i <= n; i++)
- {
- value_1 = constant_c * (pow(constant_a, i) - pow(constant_b, i));
- value_2 = (int)value_1;
- printf("%d ", value_2);
- }
- int value =constant_c * (pow(constant_a, n) - pow(constant_b, n));
- printf("\n第%d个月能生产%d只兔子\n", n, value);
- return 0;
- }
- else
- {
- return -1;
- }
- }
-
- int main(void) {
- int n;
- printf("请输入月数:");
- scanf("%d", &n);
-
- fib(n);
-
- return 0;
- }
运行结果如下:
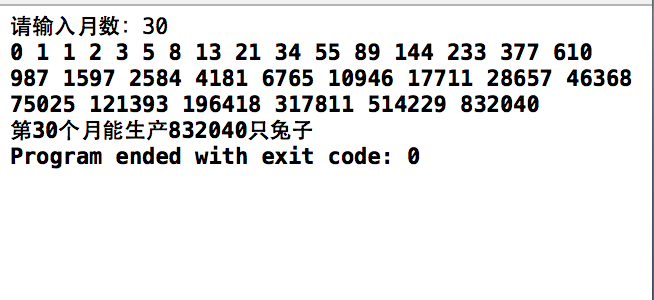
啊快去试试吧~
| 


 老版主限定
老版主限定
 沪公网安备31011502402448
沪公网安备31011502402448