【掌控】学画正弦曲线和余弦曲线

因为这张图片

有几天

玩掌控的伙伴都在用掌控玩数学

正弦余弦抛物线

……

发了不少优秀的帖子

感谢他们

终于

我也可以写一个正弦和余弦的帖子出来了

【正弦和余弦】了解一下

按古代说法

      正弦是股与弦的比例

      古代说的"勾三股四弦五"中的"弦",就是直角三角形中的斜边. 股就是人的大腿,长长的,古人称直角三角型中长的那个直角边为"股".正放的直角三角形,应是大腿站直.

      正弦是股与弦的比例,余弦是余下的那条直角边与弦的比例.

      正弦 等于 股长 除 弦长

      勾股弦放到圆里. 弦是圆周上两点联线. 最大的弦是直径. 把直角三角形的弦放在直径上,股就是长的弦,即正弦,勾就是短的弦,即余下的弦--余弦.

      正弦是六个锐角三角函数之一，其余五个是余弦(cos)和正切(tan),余切(cot)以及正割(sec)，余割(csc)。

现代说法

      正弦 等于 股长 除 弦长(即直径).

      按现代说法,正弦是直角三角形的对边与斜边之比.

      现代正弦公式是

      sin(a) = 直角三角形的对边比斜边

      放到圆里,斜边r为半径,对边y平行Y向,邻边x平行X向.

      斜边与邻边夹角a

      sin(a) = y / r

      无论y>x 或 y<=x

      无论a多大多小.

1

简单的正弦波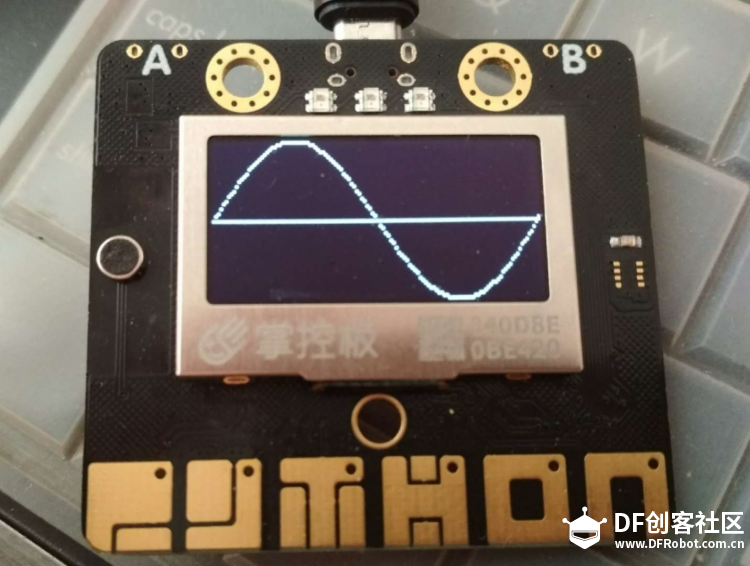

手写分析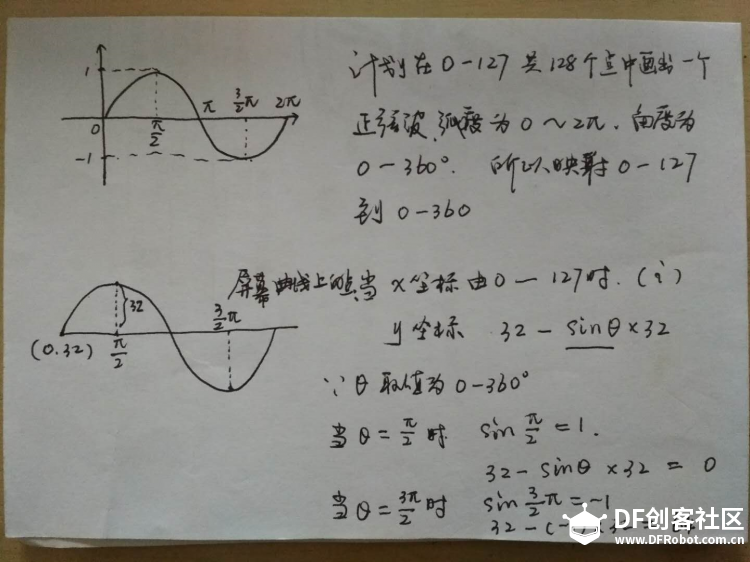

程序

逐点描绘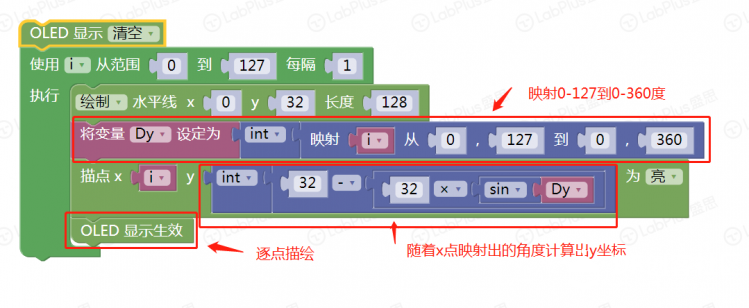

一次绘成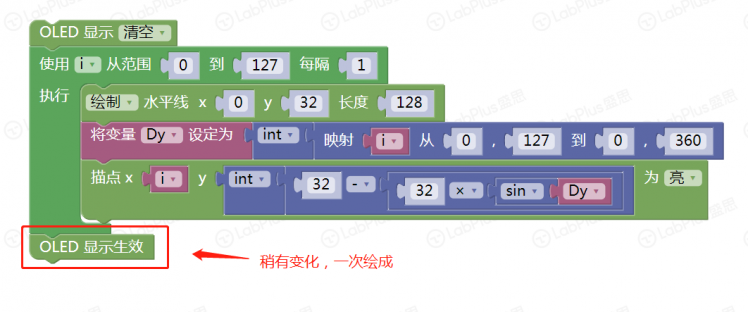

改下程序

余弦波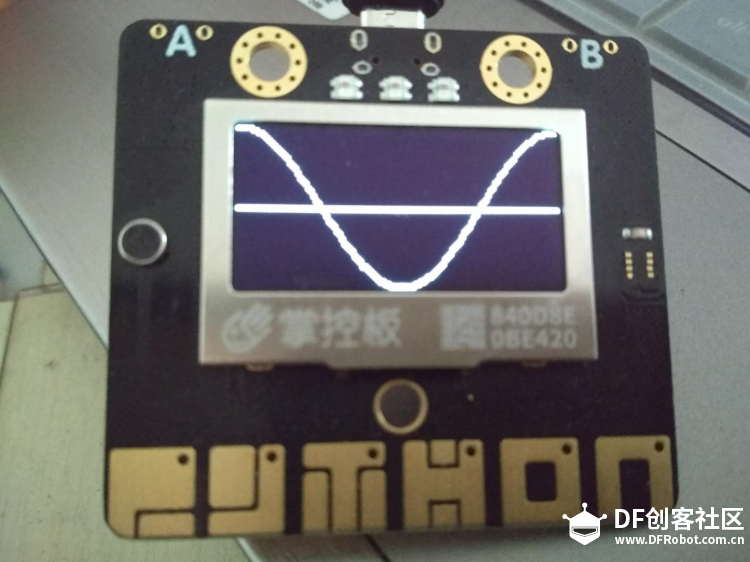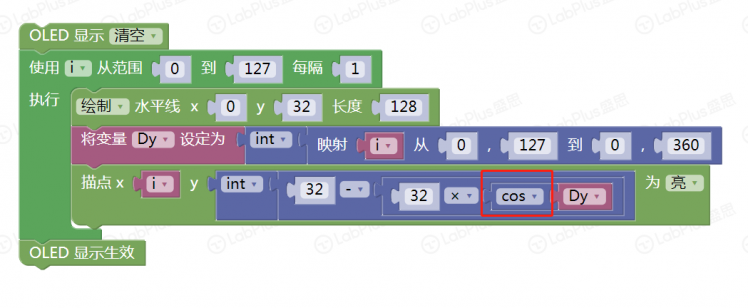

下面变化以正弦为主

【振幅】

       振幅是指振动的物理量可能达到的最大值，通常以A表示。它是表示振动的范围和强度的物理量。

       在机械振动中，振幅是物体振动时离开平衡位置最大位移的绝对值，振幅在数值上等于最大位移的大小。振幅是标量，单位用米或厘米表示。振幅描述了物体振动幅度的大小和振动的强弱。

       在交流电路中，电流振幅或电压振幅是指电流或电压变化的最大值，也叫电压或电流的峰值。

       在声振动中，振幅是声压与静止压强之差的最大值。声波的振幅以分贝为单位。声波振幅的大小能够决定音强。

       简谐振动的振幅是不变的，它是由谐振动的初始条件(初位移和初速度)决定的常数。谐振动的能量与振幅平方成正比。因此，振幅的平方可作为谐振动强度的标志。强迫振动的稳定阶段振幅也是一个常数，阻尼振动的振幅是逐渐减小的。

【周期】

       对于一个函数f(x)=Asin(ωx+φ)，函数f(x)的最小正周期是T=2π/|ω|.

       正弦交流电完成一次循环变化所用的时间叫做周期，用字母T表示，单位为秒(s)。显然正弦交流电流或电压相邻的两个最大值(或相邻的两个最小值)之间的时间间隔即为周期。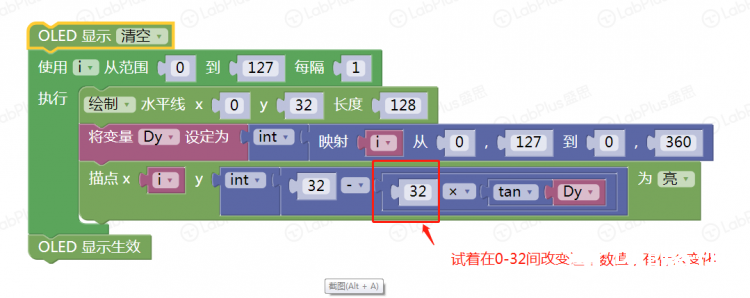

如果要做一个变化振幅的正弦波

如何改程序

增加一个for循环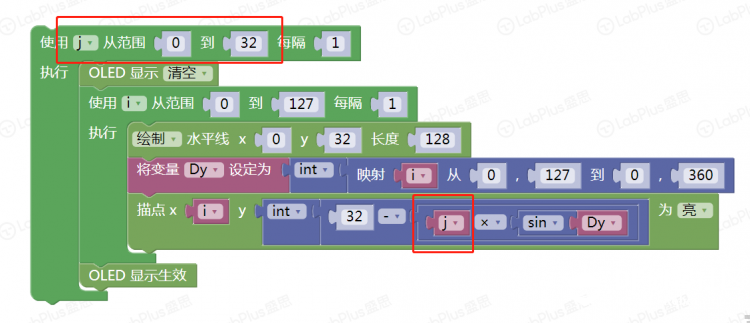

运行一下试试看

下面尝试在掌控上画出更多正弦波

想一想，改在那里动手

对于一个函数f(x)=Asin(ωx+φ)，函数f(x)的最小正周期是T=2π/|ω|.

本例中我们用最简的，f(x)=Asin（x），周期是2π

在下面标记处动手是正确的选择，改成2倍，3倍……试试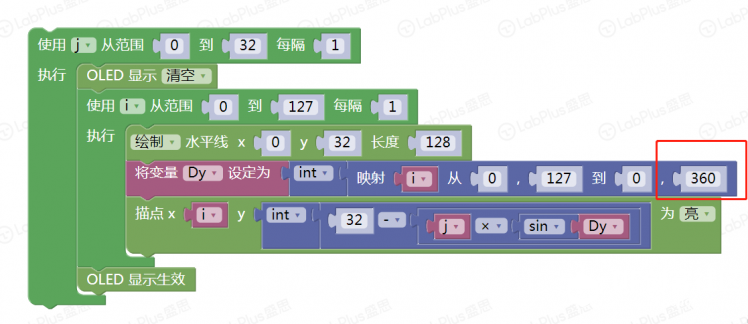

可以这样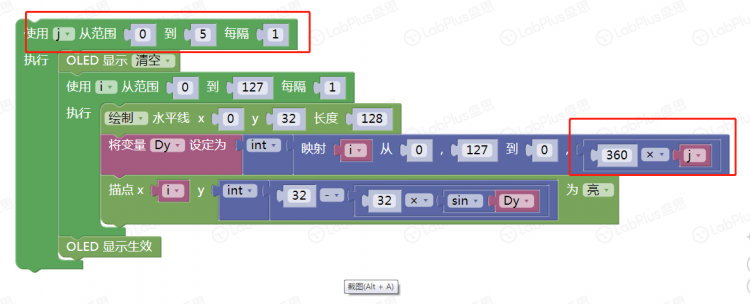

其它各种花样自己来做吧

最后给个问题，请做个能用A，B按钮调节周期数的玩法来吧。

我认真回忆了好久这些数学知识哈哈哈哈

KIKIYA 发表于 2019-2-13 23:04
我认真回忆了好久这些数学知识哈哈哈哈

KIKI，数学果真有趣，可是你的文字更美妙。
2019，注定是暗流涌动奋力前行的一年。:$