用 PID 算法玩转 3 路灰度传感器巡线小车

用 PID 算法玩转 3 路灰度传感器巡线

前言

巡线小车是学习 PID 控制的经典入门项目。本教程聚焦 3 路灰度传感器 的使用，结合 PID 算法实现精准的线性跟踪控制。通过对传感器数据的解析、误差的计算以及 PID 参数的调试，你可以掌握这一经典控制算法的实际应用。

---

一、灰度传感器与误差计算

灰度传感器通过检测地面的黑线或白线返回数值，我们可以利用这些数据推断小车相对于轨迹的偏移情况。

传感器状态与误差值

我们假设 3 路灰度传感器从左到右为 L1、M 和 R1。检测逻辑如下：

• 1 表示检测到黑线。
• 0 表示检测到白色。

根据传感器状态，定义误差值如下表：

传感器状态（L-M-R）	状态描述	偏差（Error）
0-1-0	在中心线上	0
1-1-0	偏左但部分在线	1
0-1-1	偏右但部分在线	-1
1-0-0	完全偏左	2
0-0-1	完全偏右	-2
1-0-1	交叉异常状态	保持上次误差
0-0-0	全部离线	保持上次误差

如果所有传感器都检测不到黑线，则延续上一时刻的误差值。

---

二、PID 控制原理

PID 控制的核心是利用传感器反馈的误差值对小车左右轮的速度进行动态调整，使其始终沿着黑线前进。

PID 控制公式

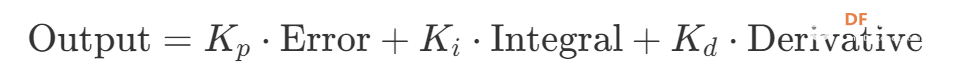
• Proportional（比例，Kp）：根据当前误差调整输出。
• Integral（积分，Ki）：对累积误差进行补偿，避免长期偏移。
• Derivative（微分，Kd）：预测误差变化趋势，减少振荡。

PID 输出值用于调整小车左右轮的速度差：

• 左轮速度 = 基础速度 - Output  
• 右轮速度 = 基础速度 + Output  

---

三、实现 PID 控制的伪代码

以下是用 Python 描述的实现逻辑，便于理解和迁移到实际硬件平台：

# 初始化 PID 参数
kp = 5          # 比例增益
ki = 0.2        # 积分增益
kd = 10         # 微分增益
base_speed = 50 # 基础速度

# 动态变量初始化
error = 0
previous_error = 0
integral = 0

# 主循环
while True:
    # 获取传感器数据
    L1, M, R1 = read_sensors()  # 返回三个传感器的状态（1 或 0）

    # 根据传感器状态计算误差值
    if L1 == 0 and M == 1 and R1 == 0:
        error = 0
    elif L1 == 1 and M == 1 and R1 == 0:
        error = 2
    elif L1 == 0 and M == 1 and R1 == 1:
        error = -2
    elif L1 == 1 and M == 0 and R1 == 0:
        error = 1
    elif L1 == 0 and M == 0 and R1 == 1:
        error = -1
    else:
        error = previous_error  # 传感器离线时保持上一误差

    # PID 控制计算
    integral += error                      # 积分
    derivative = error - previous_error    # 微分
    output = kp * error + ki * integral + kd * derivative  # PID 输出

    # 计算左右轮速度
    left_speed = max(0, min(255, base_speed - output))  # 限定在 [0, 255]
    right_speed = max(0, min(255, base_speed + output))  # 限定在 [0, 255]

    # 设置电机速度
    set_motor_speed(left_speed, right_speed)

    # 更新上一误差
    previous_error = error

---

四、参数调试方法

调试 PID 参数是确保小车平稳巡线的关键。

1. 调整 Kp（比例系数）

• 作用：对当前误差的快速修正。
• 调试：
  • 从小值（如 2）开始逐步增大。
  • 若小车响应迟缓，增加 kp；若转弯时振荡过大，减小 kp。

2. 调整 Ki（积分系数）

• 作用：修正长期偏差。
• 调试：
  • 初始设为零，观察小车是否有明显偏移。
  • 若存在跑偏问题，逐步增加 ki。

3. 调整 Kd（微分系数）

• 作用：减少振荡。
• 调试：
  • 从零开始，若小车振荡过大，逐步增大 kd。

---

五、调试案例与建议

案例 1：小车振荡过大

• 原因：kp 或 kd 过高。
• 解决：
  • 减小 kp。
  • 增加 kd 使小车转向更平滑。

案例 2：小车无法及时回到黑线上

• 原因：kp 或基础速度过低。
• 解决：
  • 增加 kp。
  • 提高基础速度（base_speed）。

案例 3：小车在直线段跑偏

• 原因：ki 未充分补偿偏差。
• 解决：
  • 逐步增加 ki，直至跑偏问题减轻。

---

六、总结

通过本教程，我们实现了基于 3 路灰度传感器的 PID 控制巡线项目，涵盖了误差计算、PID 算法实现及参数调试全过程。希望你能从中学到 PID 控制的精髓，并将其应用到更多有趣的项目中！

先点个赞