查看: 10126|回复: 3

[人工智能机器人学导论] 12 度量路径规划

上一章节：《人工智能机器人学导论》-11 导航-拓扑路径规划

《人工智能机器人学导论》-12 度量路径规划

度量路径规划（定量导航）方法通常采用根据某些最优标准产生出最优的结果，拓扑路径规划（定性导航）方法则通过可辨识路标或路口生产路径。
另外度量方法把路径分解成一系列由路途点（waypoint）组成的子目标，路途点经常是一个固定的位置或者坐标（x，y）。这些坐标可能有数学意义，但也可能在实际环境中没有与之对应的可感知物体或路标。拓扑导航只关注那些能够改变技巧运行方向的路口或位置子目标点。

度量路径规划由两个部分组成：表示部分（数据结构）和算法部分，规划器首先把环境按照适于路径规划的结构进行划分。环境描述的目的是表示环境显著特征，或者表示感兴趣的空间中与导航相关的物体有关结构，因此称之为结构空间。然后路径规划算法将规划视为图搜索问题或视为图着色问题进行计算导航。

结构空间
结构空间是一种数据结构用于描述实际的环境空间。好的结构空间表示法要尽量减少规划算法中需处理的数据维度。
六维度数据精确表示一个物体位置和姿态，其中某个坐标系中的（x，y，z）坐标来确定物体的位置，欧拉角（Euler）： Φ（俯仰角pitch）、θ（偏航角yaw）、 γ（滚转角roll）。
但是在大多数地面机器人的路径规划中并不需要六维，如果所有物体和机器人都在地面，z（高度）也可以不要。
通常移动机器人的度量路径规划及其定位都假设只有两维。机器人的模型也考虑为可原地转弯的圆形。
12 度量路径规划图1

6自由度环境空间降为两自由度结构空间

结构空间表示法
常用的结构空间表示法：Voronoi图、正则网路（regular grid）、四叉树（和他的三维扩展：八叉树）、顶点图以及自由空间与顶点图的混合法，这些表示为自由空间的划分提供了不同的方法，自由空间是指没有被物体占据的开放空间。在自由空间中机器人不会碰到任何障碍物，可自由移动。每个区域可加上 “该区域多山”，“早上9点到下午5点禁止入内”等这样的附加信息。

牧场地图
牧场地图将先验地图的自由空间转化成凸多边形，凸多边形有一个重要的性质：如果机器人从边界上认一点沿直线轴线边界上任何其他一点，它不会走到多边形之外。多边形就表示机器人游走的一个安全区域。路径规划问题就变成求解机器人所穿过多边形的最优序列问题。

下图是一个度量布局图，规划器根据机器人的尺寸相应增加障碍物的大小。规划器就可以将机器人看作一个点，而不是一个二维物体。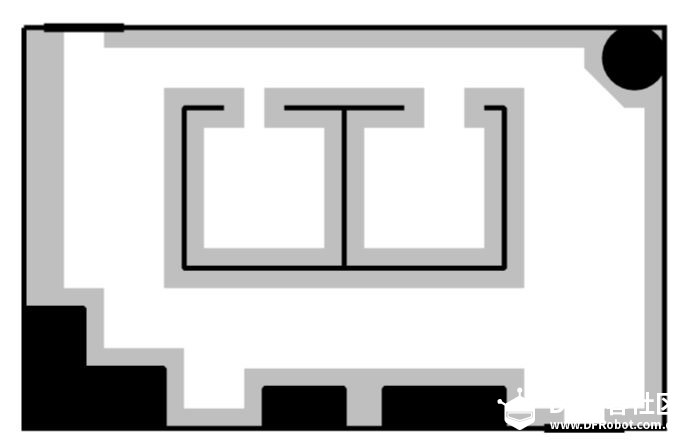
12 度量路径规划图2

接下来通过感兴趣的特征点之间的线段来构造凸多边形，这些特征点通常是：角落、门道、物体的边界等。如下图a。
然后将多边形的每个边中心点相连，如下图b。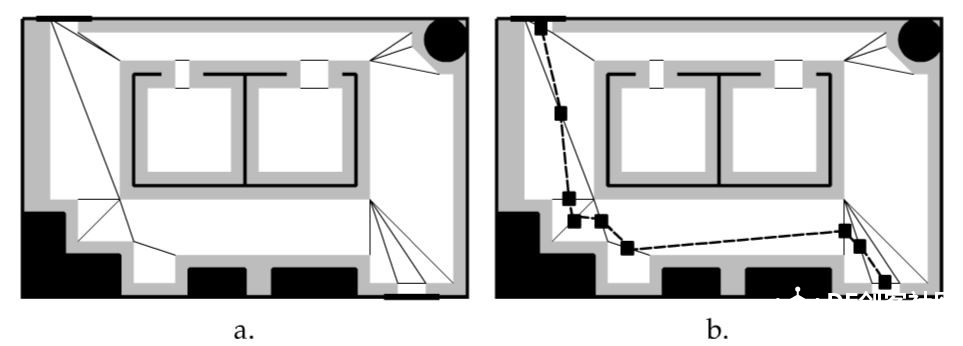
12 度量路径规划图3

但图b规划出来的路径存在锯齿状，不是最短路径。

下图设想路径是一条细绳，然后拉绳子的两端，这样可在不影响凸多边形安全区域性质的情况下从路径中删掉大部分的锯齿。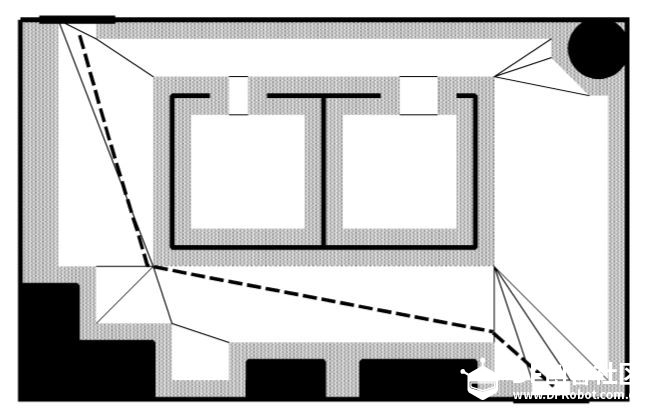
12 度量路径规划图4

牧场地图中有三个问题限制了它的可用性。第一个是多边形生成方法计算上比较复杂。
第二点是它采用地图上的人为标志而不是可以感觉到的自然物体来决定多边形的边界，除非机器人能够准确定位，否则它怎么知道沿着一条漫长没有特征的走廊走了一半并且应该旋转30度？
第三个缺点是当机器人方向先验地图和实际地图环境不符实如何更新或修正地图。

广义Voronoi图法
广义Voronoi图（Generalized Voronoi Graph），或简称GVG，是表示结构空间和产生图的一种常用机制。与牧场地图不同，机器人可以在进入新环境时临时构造GVG，从而创建一个拓扑图。
GVG的基本思想是产生与所有边界点等距离的线。这些线叫做Voronoi边。
下图这些线的走向是沿着走廊或开口的中间，Voronoi边之间交汇的点称为Voronoi顶点。因有一个与所有障碍物均保持等距离的局部控制策略，机器人可以很容易的沿着GVG产生路径前进。 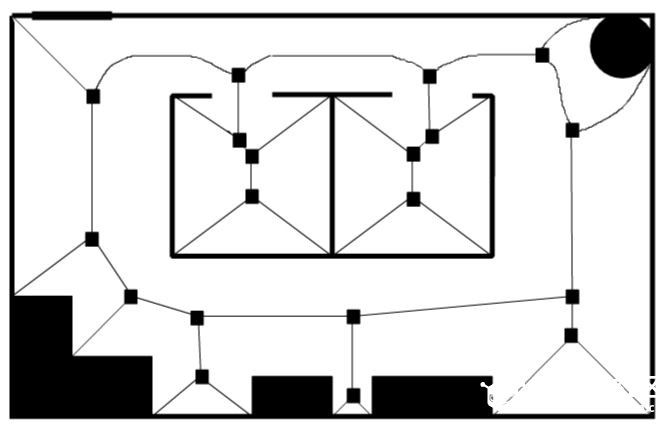12 度量路径规划图5

因为机器人一致呆在道路的中间行走，所以不需要确定具体的障碍物边界了。

正则网格法如下图正则网格法是在环境空间上覆盖一个二维笛卡尔网格，如果区域中的物体位于某个网格单元上，这个网格就标记为被占用。因此正则网格也常常称为占用网格。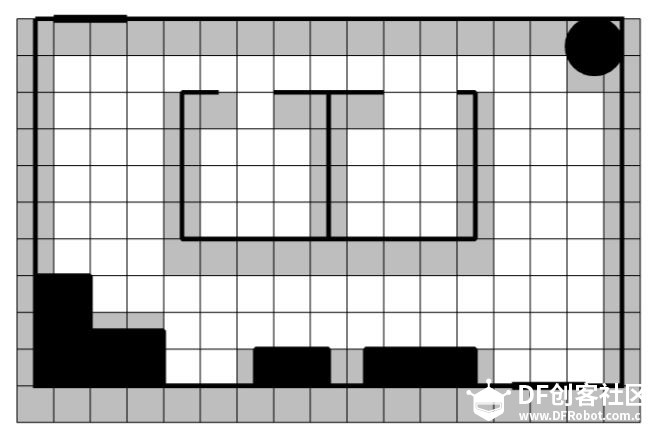
12 度量路径规划图6

正则网格用起来比较简单，把网格中的每个单元中心作为一个节点，相邻节点相连，就形成一个高维度连接图。网格即可考虑为4连接也可以考虑为8连接。

它的缺点是数字化偏差：即使物体仅仅占用了单元网格的很小一部分，整个单元都将被标记为被占用。这将导致自由空间的浪费并使物体的形状参差不齐。
为了减少空间浪费，需要将网格单元的尺寸控制到很小，大约是4-6平方英寸（25-40平方厘米），但是如此精细的单元颗粒需要很大的存储空间。需要处理的节点量会很大。

四叉树法作为正则网格法的一个变种，在避免空间浪费方面做了改进。四叉树是一种递归网格，先用较大的网格单元（8 X 8 = 64平方英寸）对区域进行划分，如果物体只占用了单元网格的一部分，结构空间算法就会把这个元素分成四个小格子（故名四叉树），每个格子16平方英寸。如果四个小格子还存在被部分占用，算法将递归的对该单元再次分割成更小的四个子单元，每个子单元4平方英寸。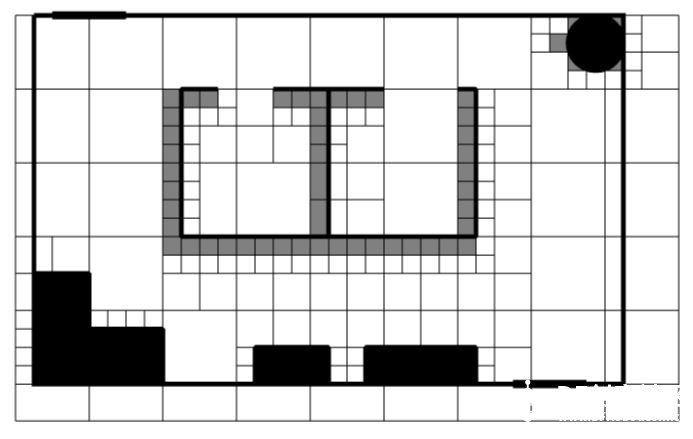
12 度量路径规划图7

基于图的规划器
从前面的部分我们可以看出，大部分结构空间表示可以转化成图的形式，这意味起始节点和目标节点之间的路径可以通过图的搜索算法来计算。图搜索算法出现于网络和路由问题，因此这一类算法从计算机科学角度看很容易理解，但其中许多算法都要求程序遍历途中的所有节点来决定起始节点和目标节点之间的最短路径。对于Voronoi图节点不多，计算并不复杂。但对于类似正则网格法的高密度连通图来说，计算复杂度变得很高。因此，人们对分支和限制型搜索算法的路径规划器非常感兴趣，该类算法能够先剔除掉那些肯定非最优的路径，算法关键的技巧在于何时进行剔除。

对于完整的机器人来说，A*（念做 A star）搜索算法是计算最优路径的经典方法。它是由A搜索算法推导出的。首先我们来举例说明A搜索算法，然后再解释A*搜索算法。两者均假设所用的是度量地图，在这个地图上，每个节点在绝对坐标系中的坐标都是已知的。图的边代表这些节点之间是否连通。
A搜索算法从起始点出发，穿过整个地图，达到目标节点，产生一个最优路径。最优路径是逐步产生的，每一步都计算所有能够加入路径的节点，并从中选择最好的一个。A搜索算法通过每次想路径中加入一个正确的节点来扩展路径，算法的核心是评估节点的可接受性的公式（或评价函数）：

f（n）= g（n）+h（n）

其中：
f（n）表示加入节点n所需的代价
g（n）表示从起始节点移动到节点n的代价。由于A搜索算法从起始节点开始向外扩展这个代价就等于已经产生的路径的距离加上从当前节点到节点n的边的距离。
h（n）表示从n节点到目标节点的最小代价
假设下面的图是有结构空间表示产生的图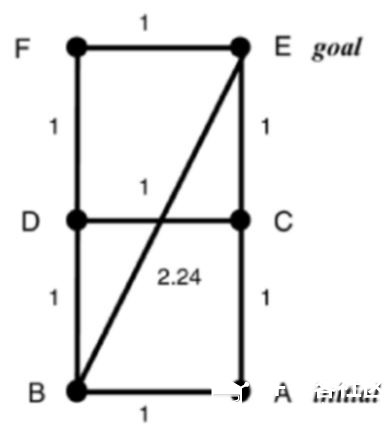
12 度量路径规划图8

A搜索算法从节点A开始，创建一个树状决策结构，当前有B和C两个节点可选择，分别计算到两点的代价
f（B）= g（B）+ h（B）= 1 + 2.24 = 3.24
f（C）=g（C）+ h（C） = 1 + 1 = 2.0
可发现到C点的代价是最低的，是最优路径。
这里假设的是美国节点h（n）都是已知的，这就意味着算法必须递归的找出h（n）的正确值，这就需要对每一个节点进行计算。

A*算法
A*算法采用一种有趣的办法来减少必须产生和比较的路径数量，该算法着重于h值的估计，而不去考虑是否实际存在这段路径能够以这个距离达到目标，然后该估计出可以于确定哪里节点更有希望最优，那些事较差的路径而可以从搜索中删除。
A*搜索算法中，评价函数变为：

f*（n）= g*（n） + h*（n）

这里*表示该函数是对A搜索算法中的相应函数的估计。

为了保证估计的准确性，不会使算法最早选择一个非最优路径，我们可以要求h*（n）永不大于h（n）。
欧几里得距离（直线距离）可以实现上面的约束要求。
结构空间图中节点位置是已知的，很容易计算出两个节点之间的直线距离。

下图例子说明了A*算法是如何减少节点访问的。同A算法一样，A*算法第一步从起始节点开始进行选择。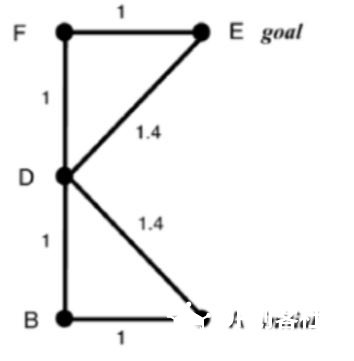
12 度量路径规划图9

f*（B）= g*（B） + h*（B） = 1 + 2.24 = 3.24
f*（D）= g*（D） + h*（D） = 1.4 + 1.4 = 2.8

这里的h*（B）和h*（D）都是直线距离，而并不需要像A搜索算法一样需要一个实际的真实路径。
路径A-D-?-E必路径A-B-?-E短的可能性更大，所以D是最具可接受性的点。注意A*算法此时不会淘汰经过B的路径，因为算法还没有找到一条从D到E的实际路径并确认它是否真的最短。
第二步，由于D是最具可接受性的点，A*算法从D开始递归调用，从D向后可选择的是E和F，计算如下：

f*（E）= g*（E） + h*（E） = 2.8 + 0 = 2.8
f*（F）= g*（F） + h*（F） = 2.4 + 1.0 = 3.4

这里计算出来的评价值是指从A出发
现在最佳路径计算出来是A-D-E,这样我们不必考虑A-B-F-E了。我们也可以优化算法，在计算到直线距离为0时停止后面的其他路径计算，因为直线距离不可能是负数。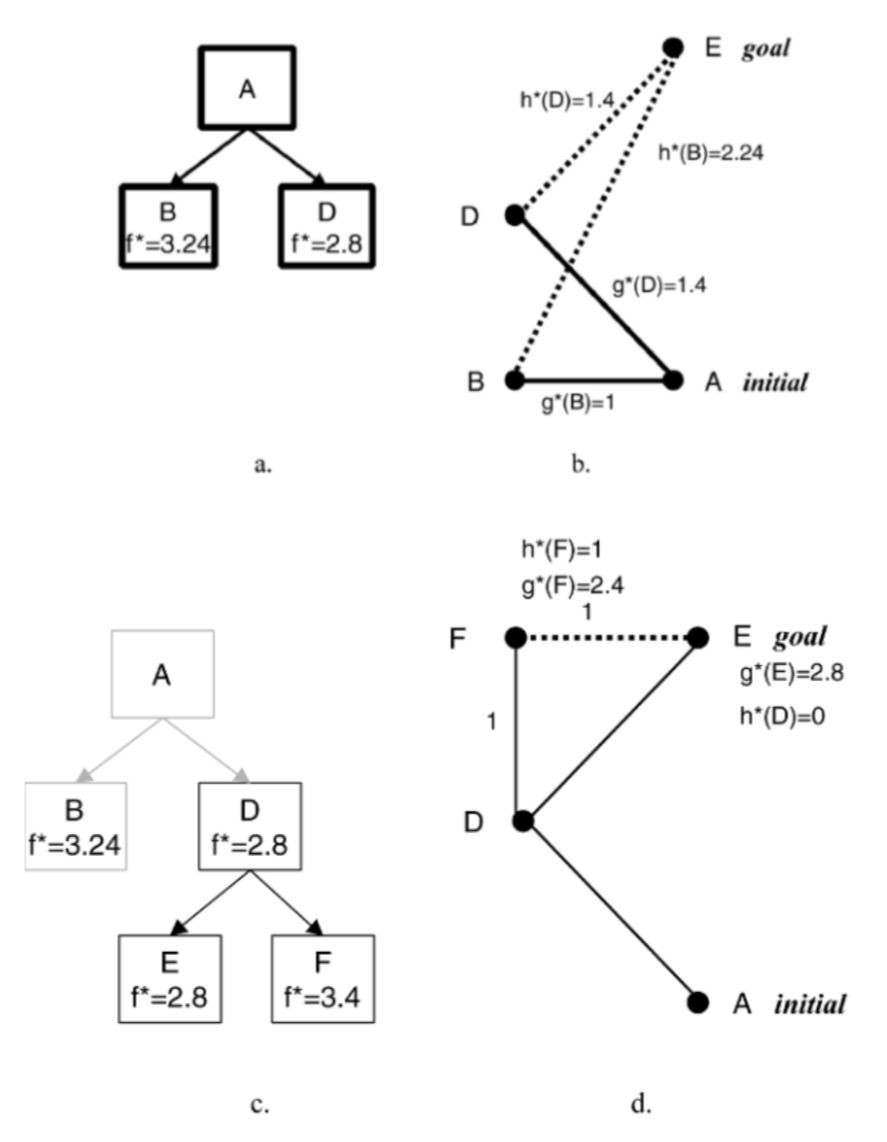

12 度量路径规划图10