本帖最后由 loria 于 2025-1-17 16:20 编辑
理论知识介绍
当谈到自然语言处理和人工智能时,词向量是一个非常重要的概念。词向量是一种数学表示方法,用于将单词或短语转化为向量形式,以便计算机能够理解和处理它们。传统的文本处理方法通常将单词表示为离散的符号,如“apple”或“cat”。然而,这种表示方式无法捕捉到单词之间的语义和关联性。词向量的出现解决了这个问题。词向量的主要思想是将每个单词映射到一个连续的数值向量空间中。在这个向量空间中,单词的语义和关联性会通过向量的相对位置和距离来表示。这意味着具有相似语义的单词在向量空间中会更加接近。现如今,有许多方法可以生成词向量。其中一种常用的方法是Word2Vec模型,它是一种基于神经网络的词向量生成模型。Word2Vec模型通过学习大规模的文本语料库来生成词向量,使得具有相似上下文的单词在向量空间中靠近。
词向量的应用非常广泛。其中一个主要的应用领域是语言模型。语言模型是指计算机对语言的概率分布进行建模的方法。通过使用词向量,语言模型可以更好地理解和生成自然语言文本。词向量和语言模型之间存在密切的关系。词向量可以用于初始化语言模型的参数,使得模型能够更好地理解文本。同时,语言模型也可以用于生成词向量,通过学习文本中的语言规律和上下文信息来生成高质量的词向量。总之,词向量是一种将单词映射到向量空间中的数学表示方法,用于捕捉单词之间的语义和关联性。它与语言模型密切相关,可以用于提升自然语言处理和人工智能任务的性能和效果 词向量可视化可以帮助我们直观地理解词之间的关系。通过在二维或三维空间中展示词向量,我们可以观察到词之间的相对位置和距离,从而推断它们的语义关系。例如,如果两个词在可视化中的位置接近,那么它们在语义上可能是相似的。通过词向量可视化,我们可以观察到具有相似语义的词被聚集在一起的现象。这有助于我们发现词义上的类别或主题。例如,如果某个区域中的词都与动物有关,那么可以推断这个区域可能是动物类别。
当想为学生讲解人工智能中有关语言模型的训练离不开词向量这一概念。但对于学生来说太过抽象而难以理解,如果能将词向量进行可视化展示,能更加直观生动,帮助学生理解。
本文分享如何通过编程使用PCA降维,实现词向量可视化表示和词与词之间的余弦相似度计算。 首先安装相应库,依次运行以下代码
- pip install xedu-python
- pip install matplotlib
- pip install scikit-learn plotly
复制代码
词向量一般为高维向量。为了可视化高维数据(比如你的256维向量)在低维空间(通常是2D或3D)的分布,常用的方法包括主成分分析(PCA)和t-SNE等方法,可以帮助我们理解数据在高维空间中的内在结构。
词向量可是会包括两步(1)编写高维向量可视化函数 (2)编写词语转向量 建立一个PY文件拷入以下代码,编写词语转向量并计算相似度 - from XEdu.hub import Workflow as wf
- import numpy as np
- from PCA import visualize_data_3d_interactive_v0
-
- # 生成词向量
- txt_emb = wf(task='embedding_text')
- words = ['king', 'man', 'queen', 'woman','people','cosmos','king is a man','queen is a']
- txt_embeddings = txt_emb.inference(data=words)
-
- # 将词向量转换为numpy数组
- vectors = np.array(txt_embeddings)
-
- # 使用PCA进行可视化
- visualize_data_3d_interactive_v0(vectors, 'd:/CODE/outputs/word_vectors.html', labels=words)
-
- # 计算余弦相似度
- def cosine_similarity(a, b):
- return np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))
-
- # 打印词向量和对应单词
- print("Words:", words)
- print("Vectors shape:", vectors.shape)
-
- # 计算并打印词向量之间的相似度
- print("\n词向量相似度矩阵:")
- for i, word1 in enumerate(words):
- for j, word2 in enumerate(words):
- sim = cosine_similarity(vectors[i], vectors[j])
- print(f"{word1} - {word2}: {sim:.4f}")
- print()
再建一个py文件填入可视化函数 - """
- PCA.py - 高维数据可视化工具
-
- 本模块提供了两种高维数据可视化方法:
- 1. visualize_data_3d_interactive_v0: 基础版本,输入为numpy数组
- 2. visualize_data_3d_interactive_v1: 增强版本,支持按类别着色和标注
-
- 功能特点:
- - 支持PCA和t-SNE两种降维方法
- - 生成交互式3D可视化图表
- - 自动保存为HTML文件
- - 支持多类别数据可视化
-
- 使用示例:
- # 基础版本
- data = np.random.rand(100, 256)
- visualize_data_3d_interactive_v0(data, 'outputs/result.html')
-
- # 增强版本
- data_dict = {
- 'class1': np.random.randn(100, 50),
- 'class2': np.random.randn(100, 50)
- }
- visualize_data_3d_interactive_v1(data_dict, 'outputs/result.html')
- """
- import os
- import numpy as np
- import matplotlib.pyplot as plt
- plt.switch_backend('agg')
- from sklearn.decomposition import PCA
- from sklearn.manifold import TSNE
- import plotly.graph_objects as go
-
-
- def visualize_data_3d_interactive_v0(X, save_path, labels=None):
- """
- 基础版本高维数据可视化函数
-
- 参数:
- X (numpy.ndarray): 输入数据矩阵,形状为(num_samples, num_features)
- save_path (str): 结果保存路径,自动添加_pca.html和_tsne.html后缀
- labels (numpy.ndarray, optional): 数据点标签,用于着色,默认为None
-
- 功能:
- 1. 使用PCA和t-SNE将高维数据降维到3D
- 2. 生成交互式3D可视化图表
- 3. 自动保存为HTML文件
-
- 返回:
- 无返回值,直接保存结果文件到指定路径
- """
- save_path = os.path.splitext(save_path)[0]
-
- # 创建outputs目录
- os.makedirs(os.path.dirname(save_path), exist_ok=True)
-
- # 动态生成颜色映射
- unique_labels = list(set(labels))
- color_palette = plt.cm.get_cmap('tab10', len(unique_labels))
- color_map = {label: f'rgb({int(color_palette(i)[0]*255)}, {int(color_palette(i)[1]*255)}, {int(color_palette(i)[2]*255)})'
- for i, label in enumerate(unique_labels)}
-
- # 将标签转换为颜色
- colors = [color_map[label] for label in labels]
-
- # 使用PCA将数据降到3维
- print('PCA is processing ...')
- pca = PCA(n_components=3)
- X_pca = pca.fit_transform(X)
-
- # 使用t-SNE将数据降到3维
- print('t-SNE is processing ...')
- tsne = TSNE(n_components=3, perplexity=3, learning_rate=200)
- X_tsne = tsne.fit_transform(X)
-
- # 为PCA结果创建一个3D散点图
- fig_pca = go.Figure(data=[go.Scatter3d(
- x=X_pca[:, 0], y=X_pca[:, 1], z=X_pca[:, 2],
- mode='markers+text',
- text=labels,
- marker=dict(
- size=5,
- color=colors, # 使用转换后的颜色
- opacity=0.8
- )
- )])
- fig_pca.update_layout(title='PCA Results', scene=dict(
- xaxis_title='Component 1',
- yaxis_title='Component 2',
- zaxis_title='Component 3'))
- fig_pca.write_html(save_path + '_pca.html')
-
- # 为t-SNE结果创建一个3D散点图
- fig_tsne = go.Figure(data=[go.Scatter3d(
- x=X_tsne[:, 0], y=X_tsne[:, 1], z=X_tsne[:, 2],
- mode='markers+text',
- text=labels,
- marker=dict(
- size=5,
- color=colors, # 使用转换后的颜色
- opacity=0.8
- )
- )])
- fig_tsne.update_layout(title='t-SNE Results', scene=dict(
- xaxis_title='Component 1',
- yaxis_title='Component 2',
- zaxis_title='Component 3'))
- fig_tsne.write_html(save_path + '_tsne.html')
-
-
- def visualize_data_3d_interactive_v1(data_dict, save_path):
- """
- 增强版本高维数据可视化函数
-
- 参数:
- data_dict (dict): 输入数据字典,格式为{类别: 特征矩阵}
- save_path (str): 结果保存路径,自动添加_pca.html和_tsne.html后缀
-
- 功能:
- 1. 使用PCA和t-SNE将高维数据降维到3D
- 2. 生成交互式3D可视化图表
- 3. 自动保存为HTML文件
- 4. 支持多类别数据可视化
-
- 返回:
- 无返回值,直接保存结果文件到指定路径
- """
- save_path = os.path.splitext(save_path)[0]
-
- # 创建outputs目录
- os.makedirs(os.path.dirname(save_path), exist_ok=True)
-
- # 准备空列表来存储所有数据点和颜色
- all_data = []
- colors = []
- pid_index = 0 # 用于为每个pid分配不同的颜色
- texts = [] # 用于存储文本标签
-
- # 提取颜色映射
- color_palette = plt.cm.get_cmap('tab10', len(data_dict))
-
- # 将每个pid的数据点收集到一起,并为第一个特征添加标签
- for pid, features in data_dict.items():
- all_data.append(features)
- colors.extend([color_palette(pid_index)] * features.shape[0])
- # 初始化所有文本为空,除了第一个特征
- texts.extend([""] * features.shape[0])
- texts[len(texts) - features.shape[0]] = pid # 为第一个特征设置pid标签
- pid_index += 1
-
- # 将所有数据合并成一个大矩阵
- all_data = np.vstack(all_data)
-
- # 使用PCA将数据降到3维
- print('PCA is processing ...')
- pca = PCA(n_components=3)
- X_pca = pca.fit_transform(all_data)
-
- # 使用t-SNE将数据降到3维
- print('t-SNE is processing ...')
- tsne = TSNE(n_components=3, perplexity=30, learning_rate=200)
- X_tsne = tsne.fit_transform(all_data)
-
- # 创建一个3D散点图显示PCA结果
- fig_pca = go.Figure(data=[go.Scatter3d(
- x=X_pca[:, 0], y=X_pca[:, 1], z=X_pca[:, 2],
- mode='markers+text',
- text=texts,
- marker=dict(
- size=5,
- color=['rgb({}, {}, {})'.format(int(c[0]*255), int(c[1]*255), int(c[2]*255)) for c in colors], # 将颜色转换为plotly格式
- opacity=0.8
- )
- )])
- fig_pca.update_layout(title='PCA Results', scene=dict(
- xaxis_title='Component 1',
- yaxis_title='Component 2',
- zaxis_title='Component 3'))
- fig_pca.write_html(save_path + '_pca.html')
-
- # 创建一个3D散点图显示t-SNE结果
- fig_tsne = go.Figure(data=[go.Scatter3d(
- x=X_tsne[:, 0], y=X_tsne[:, 1], z=X_tsne[:, 2],
- mode='markers+text',
- text=texts,
- marker=dict(
- size=5,
- color=['rgb({}, {}, {})'.format(int(c[0]*255), int(c[1]*255), int(c[2]*255)) for c in colors], # 将颜色转换为plotly格式
- opacity=0.8
- )
- )])
- fig_tsne.update_layout(title='t-SNE Results', scene=dict(
- xaxis_title='Component 1',
- yaxis_title='Component 2',
- zaxis_title='Component 3'))
- fig_tsne.write_html(save_path + '_tsne.html')
-
-
-
复制代码
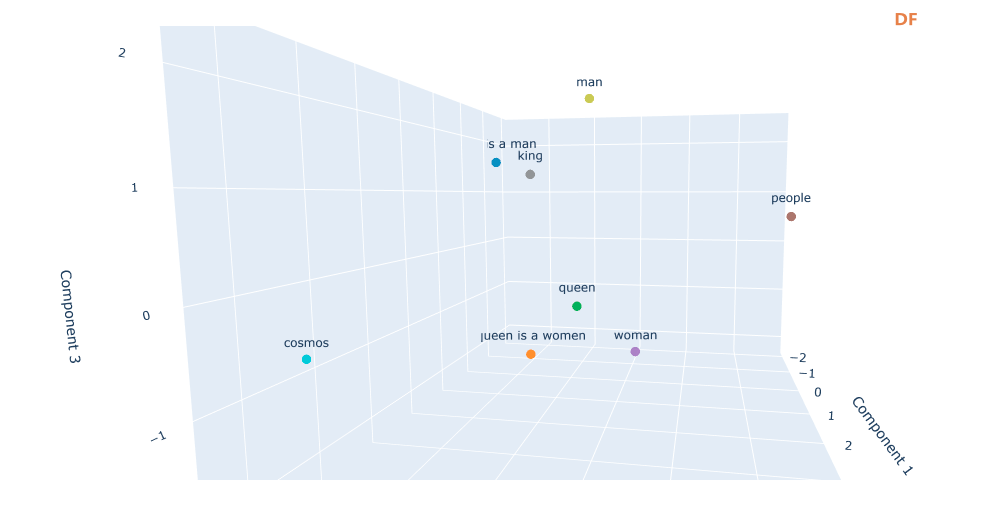
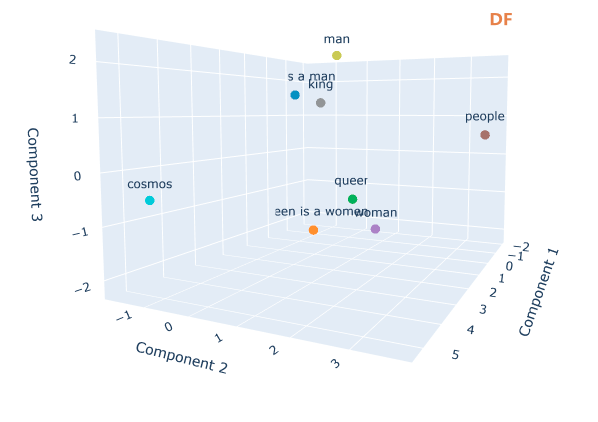
运行后生成一个文件“word_vectors_pca.html”,打开文件可以观察效果
查找终端的输出,可以观察词与词之间的余弦相似度,余弦相似度越高,词义越接近
|


 编辑选择奖
编辑选择奖
 沪公网安备31011502402448
沪公网安备31011502402448