查看: 14460|回复: 13

[入门教程] 写给设计师的趣味编程指南－（4）让图形跑起来（下）

[复制链接]

本帖最后由 kaka 于 2017-8-18 08:24 编辑

运动与函数

在大多人的印象里，数学好像没什么用，在日常生活里用得最多的也仅仅是加减乘除。

但如果你是在用程序做创作，情况就大不一样。了解越多，越能玩出花样。

先搬上几张的不明觉厉的图挑逗下大家的兴致。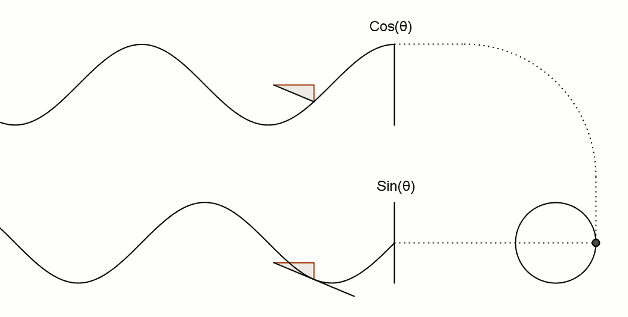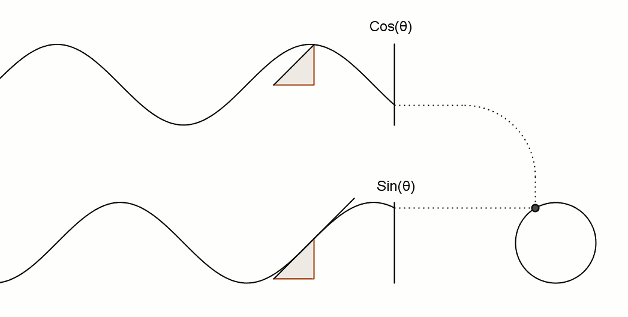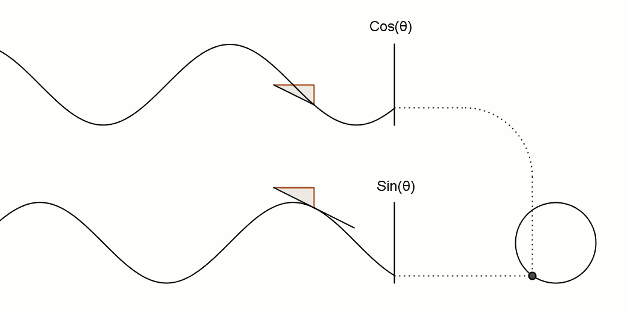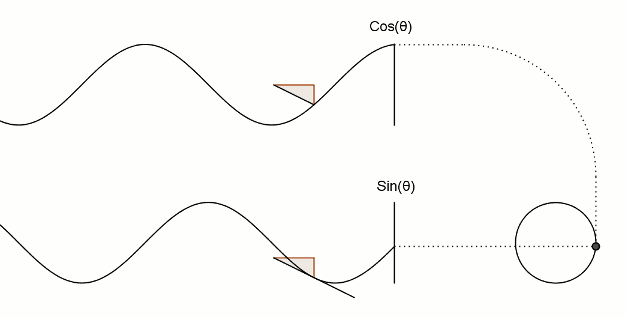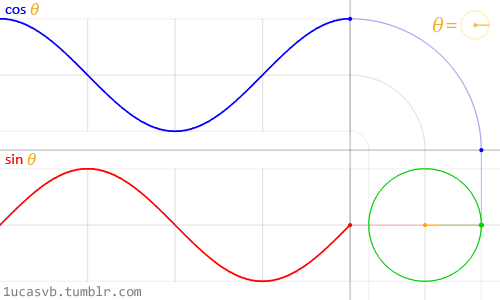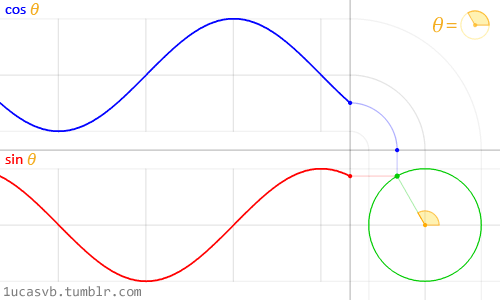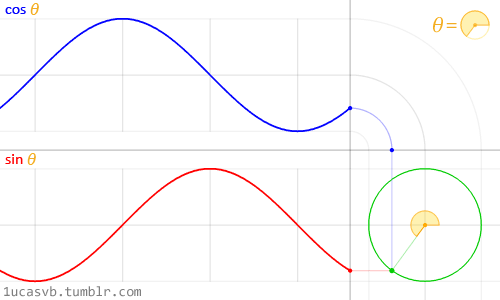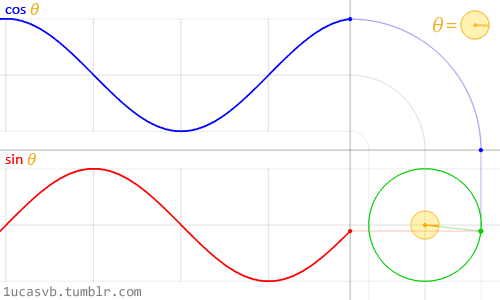

这是什么？先不剧透，后面你会亲自用上它。

上一节，我们了解了 setup 函数和 draw 函数，这使得静止的图形可以运动起来。只是这种运动形式太朴素了。我们要用上以前掌握的函数知识，让图形跑出自己的个性。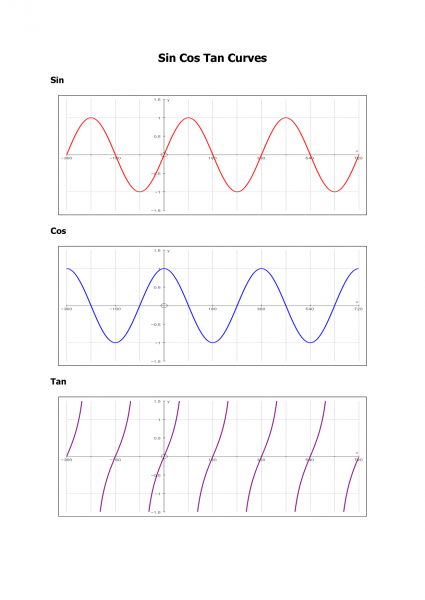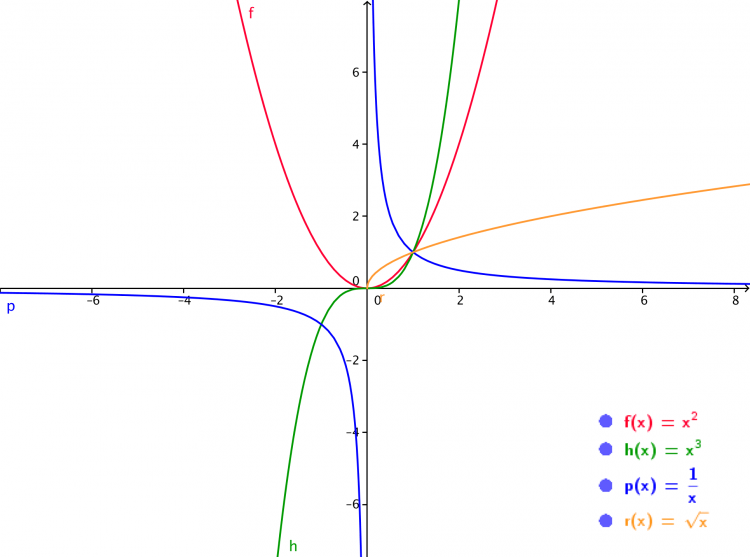

上面的数学函数还能认出多少？它们与运动究竟有什么关系？

就先从里面挑一个二次函数，再随便加些参数看看，比如 y = x² / 100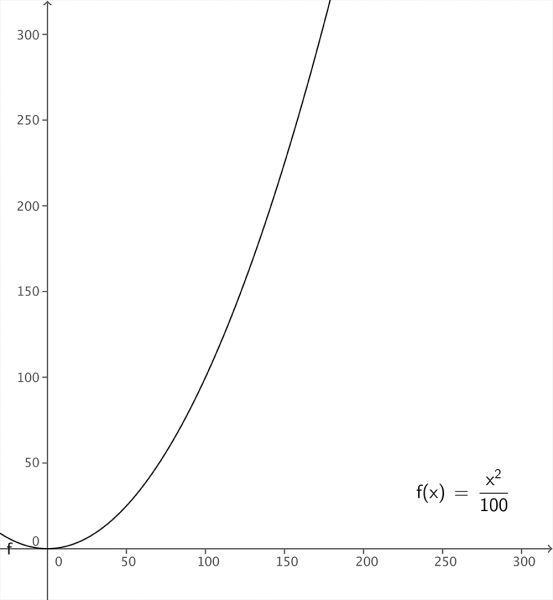

它的函数图像是这样的，复制下面这段代码

[mw_shl_code=applescript,true]float x, y;
void setup(){
size(300, 300);
background(0);
x = 0;
}
void draw(){
stroke(255);
strokeWeight(2);
y = pow(x, 2) / 100.0; //pow函数会返回指定数的n次方（x,2）代表 x的平方，第一个参数是底数，第二个参数代表指数
point(x, y);
x++;
}[/mw_shl_code]

运行效果。

接着再挑个 sin 函数, y = 150 + sin(x)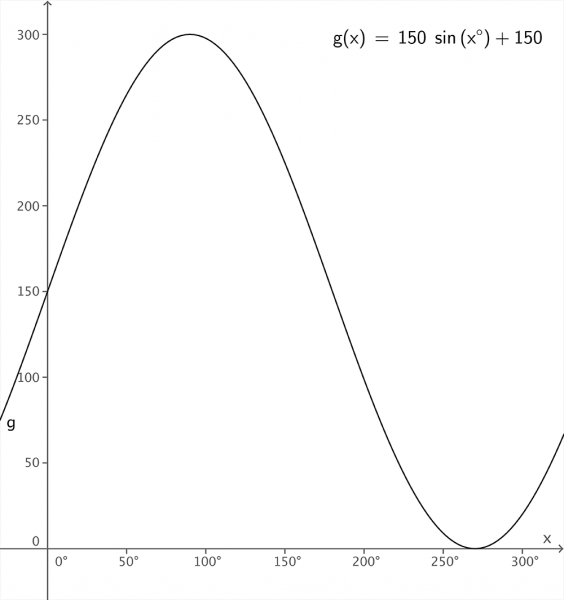

复制下面这段代码。

[mw_shl_code=applescript,true]float x,y;
void setup(){
size(300, 300);
background(0);
x = 0;
}
void draw(){
y = height/2 + sin(radians(x)) * 150; //radian函数将x转换为角度
x++;
stroke(255);
strokeWeight(2);
point(x, y);
}[/mw_shl_code]

运行出来的图形是这样的。

这就是它们的运动轨迹了。对照着上下两张图，结果是显而易见的。函数图像其实就对应着运动轨迹！相当简单，只要将x，y的值替换进坐标中就行了。第一张绘制的轨迹，其实就等价于函数 y = x² / 100 的图形。而第二张的轨迹，等价于 y = 150 + sin(x) 。只是在程序中，y轴方向是反的，所以与原图相比，图形轨迹会是上下颠倒。

现在应该有种阔然开朗的感觉！以前学习的各式稀奇古怪的函数，原来是可以用来控制图形的运动！

函数怎么写？

下面罗列了一些使用频率很高的函数，这可以帮助我们将数学函数翻译成计算机能识别的代码

[td]

函数名	作用	格式
abs	返回指定数的绝对值	abs（x)
log	返回以自然对数 e 为底，n 的对数	log(n)
sq	返回指定数的平方根	sq(x)
sqrt	返回指定数的平方根	sqrt(x)
pow	返回指定数的 n 次方	pow(x,n)
exp	返回自然对数 e 的 n 次方	exp(n)

因此下面这些式子，在程序中就可以这样写。

y = x² → y = pow(x, 2) 或 y = sq(x)

y = x³ → y = pow(x, 3)

y = xⁿ → y = pow(x, n)

y = 4ⁿ → y = pow(4, n)

y ＝logₑ² → y = log(2)

y = e² → y = exp(2)

y = √5 → y = sqrt(5)

你也可以随便在程序里写个函数，看看它的运动轨迹是怎样的！但记得要考虑函数的值域和定义域的范围，否则你画的图很可能会跑在屏幕之外。

三角函数

下面再深入地了解一下与三角函数相关的函数写法

[td]

函数名	作用	格式
sin	正弦函数	sin（x)
cos	余弦函数	cos（x)
tan	正切函数	tan（x)
radians	将角度值转化成弧度值	raidans(x)
degrees	将弧度值转化为角度值	degrees(x)

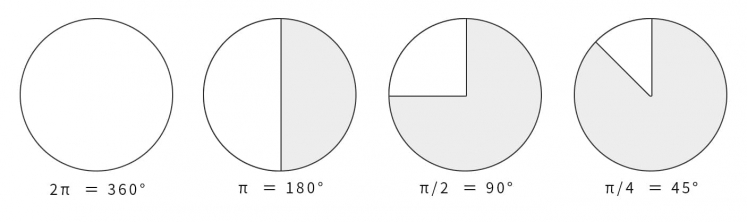值得注意的是，在程序中，与角度相关的函数参数输入采取的是弧度制。所以 sin90° ，应该写成 sin（PI／2）。如果不熟悉这种方式，也可以用 randians 函数将角度先转换为弧度，写成 sin（radians(90))。

degrees函数的作用恰恰相反，可以将弧度值转化为角度值。在编辑区内直接输入 print(degrees(PI/2)); 看看结果会是多少？

用三角函数控制图形运动

下面给出一个范例，看看实际的图形运动效果

[mw_shl_code=applescript,true]float x, y;
void setup(){
size(700, 300);
}
void draw(){
background(234, 113, 107);
y = sin(radians(x)) * 150 + 150;
x++;
noStroke();
ellipse(x, y, 50, 50);
}[/mw_shl_code]

sin函数是周期函数，最小值是－1，最大值为 1 。屏幕高度为 300 。根据 y = sin(radians(x)) * 150 + 150 ，因此 y 值的变化范围就会刚好控制在 0 到 300 之内。

旋转的圆

好了，这节的重头戏终于到了。那我们怎么在程序中画一个圆的轨迹呢？应该怎么用函数去表示？再次搬出这两张图～～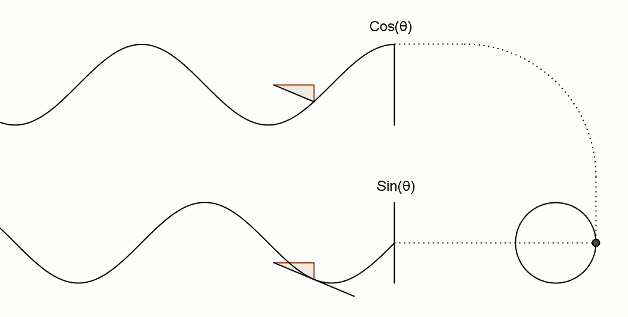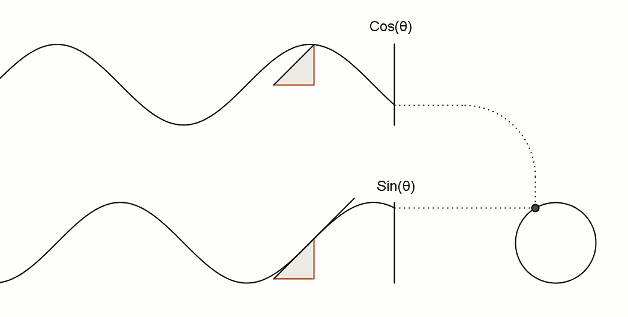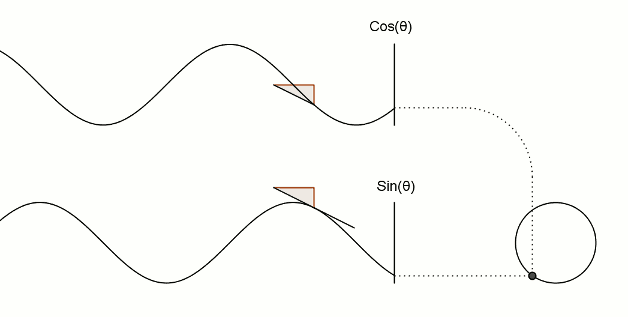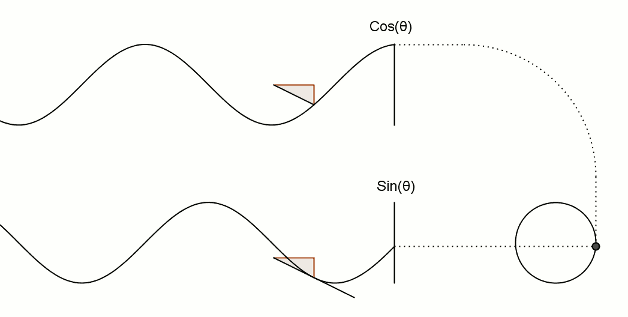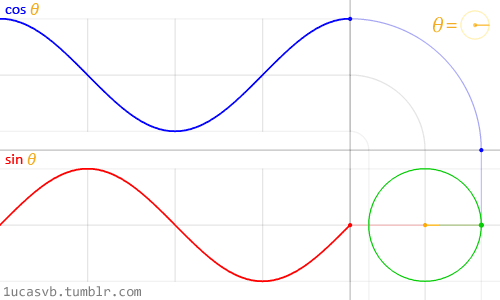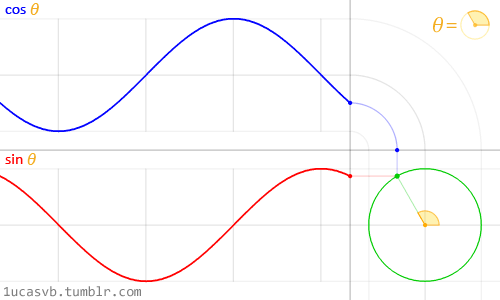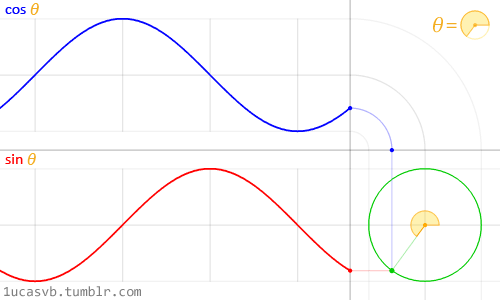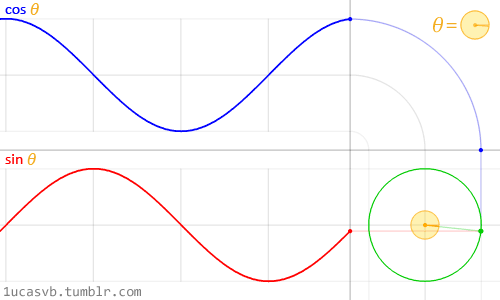

它们其实很直观地揭示了圆周坐标与三角函数的关系。图上所有的运动，都是通过不断增大自变量 θ 来驱动的。左边其实就是 sin 函数与 cos 函数的图像，右边代表的是经过映射后，一个作圆周运动的点。是不是很巧妙！现在看一点也不神秘了，你还可以用代码去实现它！

例子十分简单：

[mw_shl_code=applescript,true]float x, y, r, R, angle;
void setup(){
size(300, 300);
r = 20; //圆的直径
R = 100; //运动轨迹的半径
x = 0;
angle = 0;
y = height/2;
}
void draw(){
background(234, 113, 107);
translate(width/2, height/2); //将原点移至屏幕中心
noStroke();
x = R *cos(angle);
y = R * sin(angle);
ellipse(x, y, r, r);
angle += 0.05;
}[/mw_shl_code]

一个旋转的圆出现了。在这里，自变量不再是不断递增的 x ，而是变成了 angle（也相当于例图中的 θ ）。它就代表角度。其中 xy 都分别乘以系数 R，也就相当于扩大了圆的运动半径（ R 代表运动半径）。若是不乘以 R ，它的图形变化轨迹只会局限在－1 到 1 的范围。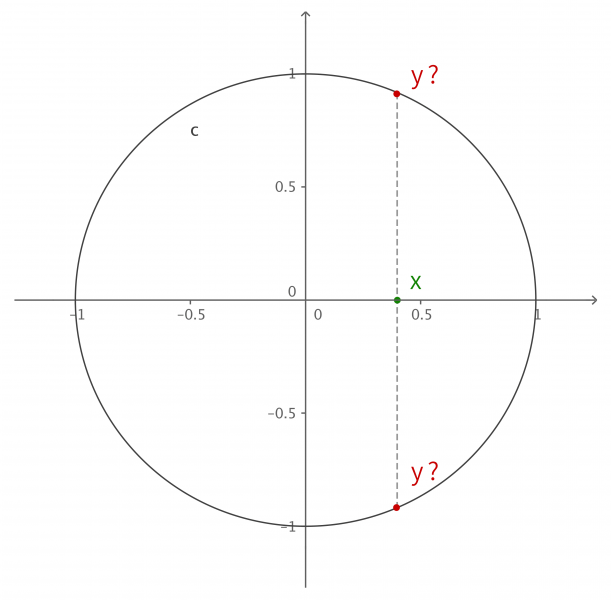

但为什么不能用不断递增的 x 呢？根据函数本身的特性,定义域中任意 x ,有且只有一个 y 与之相对应。所以在平面直角坐标系里，你无法找出一个“简单函数”直接画出圆。

也就是不能再用这种形式

y = (包含x的神秘表达式？) ；
x＋＋；

所以才需要拐个弯，找一个 angle 来作为自变量。再用 sin 和 cos 函数将它转化为横纵坐标。

x = R * cos(angle);
y = R * sin(angle);
angle += 0.05;

可能又有人会好奇，为什么这样就能表示圆的轨迹呢？根据三角函数的定义其实是不难推出的。sin 函数是对边与斜边之比，cos 函数是邻边与斜边之比。无论圆周上的点位置在哪，r（半径）都是不变的。因此可以得到 x 坐标与 y 坐标的表达式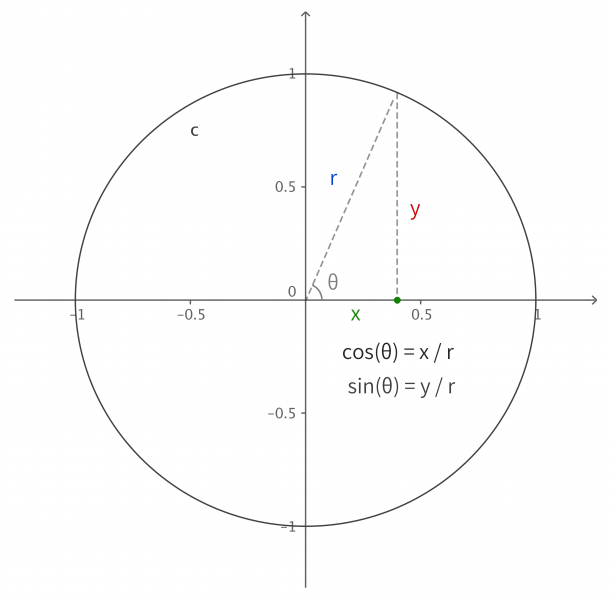

由于这个不是数学指南，有关三角函数的知识，就不在这里展开了。如果确实忘记，可以再去回顾一下。

当然啦，不完全理解也没有问题，只要知道怎么用它画圆就可以了。这也是一种“编程思维”，以后我们常常需要调用一些别人做好的模块来实现某种功能。所以无需有强迫症的心态，非要搞懂里面的细节。

但 sin 和 cos 还是相当常用的，如果你想进行更高阶的创作，尽量想明白。若是这个问题本身能促使自己去了解更多数学知识，那就更好了，后面会有更多有意思的东西等你去挖掘。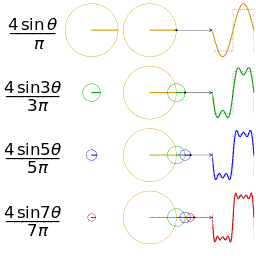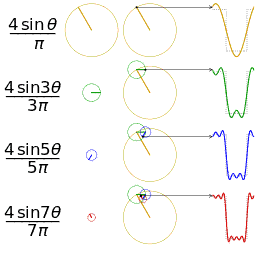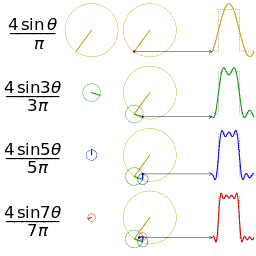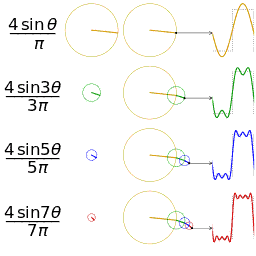

就像这几张动图，其实都与三角函数密切相关。

运动的坐标系

之前的效果，都是图形坐标在变化，坐标系本身是静止的。其实我们可以通过让坐标系动起来，来实现运动效果。这就好比岸上的人看船上的人，船上的人相对船是静止，但若是船本身在动，从岸上看去，人也就动了。所以前面讲的例子，一直都是“人在船上跑”，船并没有动。

下面是变换坐标系的常用函数

[td]

函数	作用
tranlate（x, y)	平移坐标系
scale(a)	缩放坐标系
rotate(a)	旋转坐标系
pushMatrix（）／ popMatrix（）	变换堆栈（存取坐标系）

translate函数

translate函数前面有提到过，用于平移图形的坐标系

调用形式：

translate(a, b)

第一个参数代表往 x 轴的正方向移动 a 个像素，第二个参数代表往 y 轴的正方形移动 b 个像素。

对比两段代码，看有何不同（为简化代码，可以不输入size函数，屏幕的宽高为默认值 100 ）

使用前：

ellipse(0, 0, 20, 20);

使用后：

translate(50, 50);ellipse(0, 0, 20, 20);

rotate函数

调用形式：

rotate(a)

函数用于旋转坐标系，当参数为正数，会以原点为中心，往顺时针方向旋转。传入的参数和三角函数一样，采取弧度制。

使用前：

ellipse(50, 50, 20, 20);

使用后：

rotate(radians(30));ellipse(50, 50, 20, 20);

在程序中产生的作用，就是使圆围绕坐标原点，顺时针旋转了 30 度。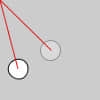

scale函数

调用形式：

scale(a)

函数可以缩放坐标系，数值代表缩放的倍数。当参数大于 1 放大，小于 1 则缩小。

使用前：

ellipse(0, 0, 20, 20);

使用后：

scale(4);ellipse(0, 0, 20, 20);

上图的圆就放大到原来的四倍了。你也可以使用两个参数，分别缩放 x 轴方向和 y 轴方向：

scale(4，2);ellipse(0, 0, 20, 20);

圆的绘制坐标可是一直没有变，变的是它的坐标系。

旋转运动[mw_shl_code=applescript,true]float r, R, angle;
void setup(){
size(300, 300);
r = 20; //圆的直径
R = 100; //运动轨迹的半径
}
void draw(){
background(234, 113, 107);
translate(width/2, height/2); //将原点移至屏幕中心
rotate(angle);
noStroke();
ellipse(0 ,R ,r ,r);
angle += 0.05;
}[/mw_shl_code]

是不是比起用三角函数画圆更简洁，也更易理解了？这里估计会有一个疑问，以旋转运动的代码为例。前面提过的变换函数明明是相对的，而且允许叠加效果。那 translate(width/2,height/2) 写在 draw 函数里，岂不代表 draw 函数每运行一次，坐标系都会在原基础上往右下方移动一段距离？按理说是不会永远保持在屏幕中心的？

你可以这样去理解，draw 函数里的代码只要由上到下跑完一次，第二次循环时坐标系都会回到始初状态，坐标系的原点会默认回到左上角上。所以要想保持坐标系的变化是持续的，rotate 函数中的 angle 参数，就需要不断递增。

存取坐标状态

有些时候，我们不希望坐标系的状态是在之前的基础上变换。这时就要用到 pushMatrix 和 popMatrix 。这两个函数是成对出现的，pushMatrix 在前 popMatrix 在后。不能单独使用，否则就会出错。

例子：

pushMatrix(); //保存坐标系状态
translate(50, 50);
ellipse(0, 0, 20, 20);
popMatrix(); //读取坐标系状态
rect(0, 0, 20, 20);

变换函数的叠加

这里的变换都是相对当前坐标系的变换。换句话说，效果是可以叠加的。

translate(40, 10);translate(10, 40);ellipse(0, 0, 20, 20);

最终效果就等价于

translate(50, 50);ellipse(0, 0, 20, 20);

由于 scale 和 rotate，都是以原点为中心进行缩放和旋转的。当我们希望一个中心位置在（50，50）的图形产生旋转的效果。就需要倒过来思考，先将坐标原点移动到（50，50）的位置，再添加旋转变换函数，最后再将图形绘制在原点上。

使用前：

ellipse(50, 50, 50, 20);

使用后：

translate(50, 50);rotate(radians(45));ellipse(0, 0, 50, 20); //为了看出旋转的角度变化，绘制一个椭圆

例子中，在使用 translate(50,50) 前，先用 pushMatrix。就会保存坐标系当前的状态，这个同时也是初始状态。当绘制了圆形后，再执行 popMatrix 。就会还原到到这个状态。此时再执行 rect ,会发现它没有受到 translate 的影响。而是在左上角的原点上绘制了一个正方形。

另外，pushMatrix 和 popMatrix 是允许嵌套使用的。

例如

pushMatrix();
…
pushMatrix();
…
popMatrix();
…
popMatrix();
…

为了更直观地表明对应关系，采取了缩进的形式

组合运动，运动中的运动？

第二波重头戏开始了。试着往前推进一步。前面用船和人的例子作比喻。有没有想过，要是船上的人和船都动起来，岸上的人看过去会是怎样的一番体验？

例如平移运动与坐标系的旋转运动组合起来?这里的点其实只朝一个方向运动哦～～

[mw_shl_code=applescript,true]int x, y;
float angle;
void setup(){
size(300, 300);
background(234, 113, 107);
noStroke();
x = 0; //当需要 x 的初始值为 0 的时候。可以不写这句代码。在声明变量时，默认值即是零
y = 0; //同上
angle = 0; //同上
}
void draw(){
angle += 0.25;
y—;
translate(width/2, height/2);
pushMatrix();
rotate(angle);
ellipse(x, y, 5, 5);
popMatrix();
}[/mw_shl_code]

还有就是圆周运动与坐标系的缩放运动。

[mw_shl_code=applescript,true]float x, y, angle;
void setup(){
size(300, 300);
background(234, 113, 107);
noStroke();
}
void draw(){
angle += 0.01;
x = sin(angle) *100;
y = cos(angle) * 100;
translate(width / 2, height / 2);
pushMatrix();
scale(1 + 0.1 * sin(angle * 10));
ellipse(x, y, 5, 5);
popMatrix();
}[/mw_shl_code]

[mw_shl_code=applescript,true]可别被它欺骗了，圆点其实只在做圆周运动。这个坐标系的缩放用摄像头去类比会较易理解，一个不断前后运动的摄像头在拍摄一个作圆周运动的点。
看完以上有没有被惊艳到了？都是简单的基础函数，但通过不同组合，效果却可以千差万别。后面我就不透露太多了，怎能剥夺大家探索的乐趣呢？
综合运用
这节快要结束了。近两节指南较详细地介绍了图形运动的基本方法。相信你对于图形的运动，比以前的理解更深了。最后给出一些完整的实例供大家参考。[/mw_shl_code]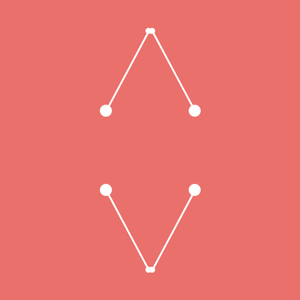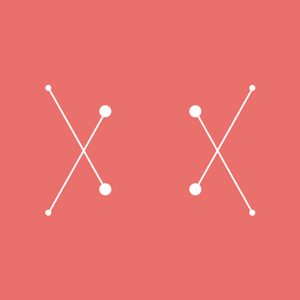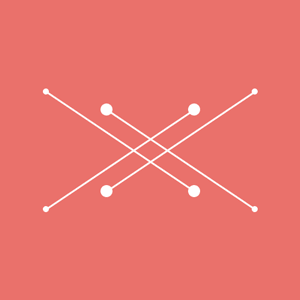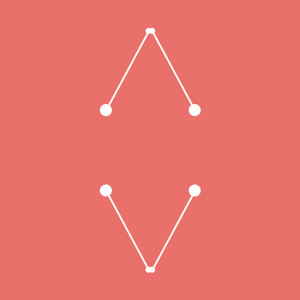

[mw_shl_code=applescript,true]float x1, y1, x2, y2, r, R;
float angle1, angle2;
void setup(){
size(300, 300);
r = 12;
R = 120;
angle1 = 0;
angle2 = PI/4;
}
void draw(){
background(234, 113, 107);
noStroke();
translate(width / 2, height / 2);
angle1 += 0.02;
angle2 += 0.06;
x1 = R *sin(angle1);
y1 = R *cos(angle1);
x2 = R/2 *sin(angle2);
y2 = R/2 *cos(angle2);
ellipse(x1, y1, r/2, r/2);
ellipse(x2, y2, r, r);
ellipse(-x1, -y1, r/2, r/2);
ellipse(-x2, -y2, r, r);
ellipse(x1, -y1, r/2, r/2);
ellipse(x2, -y2, r, r);
ellipse(-x1, y1, r/2, r/2);
ellipse(-x2, y2, r, r);
stroke(255);
strokeWeight(3);
line(x1, y1, x2, y2);
line(-x1, -y1, -x2, -y2);
line(x1, -y1, x2, -y2);
line(-x1, y1, -x2, y2);
}[/mw_shl_code]

这个例子涉及的函数知识都没有超出前面的。

是不是搞不清哪个点对哪个点？哪条线对哪条线？其实我自己也搞不清楚……但我还记得它是由一小段代码衍生而来的。

这就是它的运动本质。其余的线条仅仅是镜像效果而已。

如果你继续跟随这个指南，后期还可以做一个升级版，给图形添加控件，来实时地改变图形的运动状态。

编程的有趣之处就在于你可以设计规则，组合规则。但最终能写成什么程序，就看自己的造化了。设计师往往有很强的图形想象力，你既可以先在脑中勾勒出动态草图，再设法从脑中“翻译”成代码。也能从代码和法则本身出发，随意设计函数和变量。请记住，Processing 就是你的 sketch ，代码则是你的画笔！用它挥洒自己的创意吧～～

END

最后穿越回去解答一个之前的遗留问题吧。我那么费力地用程序画一张图，究竟有啥用？学完这章以后，有太多玩法了。

[mw_shl_code=applescript,true]float browX, earD, eyeD, faceD;
void setup(){
size(500, 500);
}
void draw(){
background(200, 0, 0);
browX = 150 + sin(frameCount / 30.0)* 20;
earD = 180 + sin(frameCount / 10.0) *20;
eyeD = 60 + sin(frameCount/30.0) *50;
faceD = 300;
strokeWeight(8);
ellipse(175, 220, earD, earD);
ellipse(width - 175, 220, earD, earD);
rect(100, 100, faceD, faceD);
line(browX, 160, 220, 240);
line(width-browX, 160, width-220, 240);
fill(random(255),random(255),random(255));
ellipse(175, 220, eyeD, eyeD);
ellipse(width-175, 220, eyeD, eyeD);
fill(255);
point(width/2, height/2);
triangle(170 - cos(frameCount / 10.0) * 20, 300 - sin(frameCount / 10.0) * 20, width - (170 + cos(frameCount / 10.0) * 20), 300 + sin(frameCount / 10.0) * 20, 250, 350);
}[/mw_shl_code]