【花雕动手做】CanMV K230 AI视觉模块之使用傅里叶变换

傅里叶变换（Fourier Transform）是信号处理、数学和物理学领域的核心工具，通过将信号从时域转换到频域，揭示其频率成分。以下是关于傅里叶变换的具体介绍：

1、基本原理
核心思想
任何信号（无论是周期性还是非周期性）都可以表示为不同频率的正弦波或余弦波的叠加。
数学表达
连续傅里叶变换（FT）：对于连续函数f(t)，其频域表示为
F(ω)=∫ −∞ ∞ f(t)e −j2πωt dt，其中ω为角频率。
离散傅里叶变换（DFT）：针对离散信号f[n]，公式为
F[k]=∑ n=0 N−1 f[n]e −j2πkn/N，
k为频率索引3。
快速傅里叶变换（FFT）：一种高效计算DFT的算法，复杂度从O(N 2 )降至O(NlogN)，广泛应用于工程实践。
主要类型
连续与离散形式
连续傅里叶变换适用于模拟信号，而离散形式（DFT/FFT）用于数字信号处理。
逆变换
从频域恢复时域信号，例如IDFT公式为
f[n]= N1∑ k=0 N−1 F[k]e j2πkn/N 。

2、应用领域
信号处理
噪声去除：通过滤除高频成分（噪声通常为高频）平滑数据。
特征提取：识别周期性信号的频率（如周期性干扰）。
适用性：适合分析时间序列数据的频率特性，平滑噪声或提取周期性模式。
图像处理与计算机视觉
频域滤波：低通滤波保留平滑区域，高通滤波增强边缘。
压缩技术：JPEG利用离散余弦变换（DCT，傅里叶变种）量化高频分量。
模式识别：频域模板匹配提升物体检测效率。
物理与工程
量子力学：波函数在坐标空间与动量空间的转换依赖傅里叶变换。
光学建模：几何傅里叶变换优化强相位波前的快速计算，应用于衍射模拟。
电路分析：谐波分析法处理非正弦交流电。
总之，傅里叶变换不仅是一种数学工具，更是连接理论与应用的桥梁。其核心价值在于将复杂问题转化为频域中的可操作问题，从而在众多领域中实现高效分析与优化。

【花雕动手做】CanMV K230 AI视觉识别模块之使用傅里叶变换
项目测试实验代码

#【花雕动手做】CanMV K230 AI视觉识别模块之使用傅里叶变换         
# 项目功能：演示在嵌入式设备上使用FFT进行频域信号分析

# 导入必要的模块
from machine import FFT  # 硬件加速的FFT模块，提供快速傅里叶变换功能
import array  # 数组模块，用于高效数值计算
import math   # 数学函数模块
from ulab import numpy as np  # 嵌入式设备优化的numpy库，提供数组操作

"""
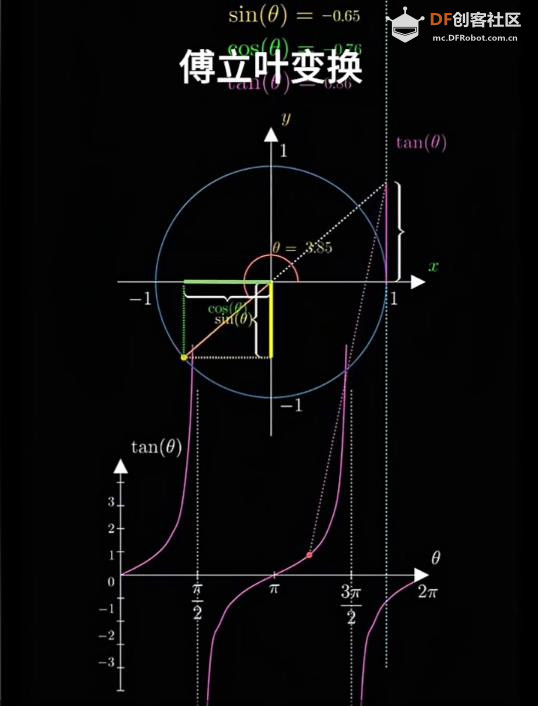
傅里叶变换(Fourier Transform)是一种将时域信号分解为不同频率正弦波的叠加的数学方法。
它可以帮助我们分析信号中包含的频率成分。FFT(快速傅里叶变换)是一种高效计算傅里叶变换的算法。

The Fourier Transform is a mathematical method that decomposes a time-domain signal into 
the sum of sinusoidal waves of different frequencies. It helps us analyze the frequency 
components contained in a signal. FFT (Fast Fourier Transform) is an efficient algorithm 
for computing the Fourier transform.

技术要点 | Technical Points:
1. 时域到频域：将信号从时间维度转换到频率维度
2. 频谱分析：识别信号中的主要频率成分
3. 应用场景：音频处理、振动分析、通信系统、图像处理等
4. 硬件加速：K230的FFT模块使用专用硬件提高计算效率
"""

# 定义圆周率常量
# Define PI constant
PI = 3.14159265358979323846264338327950288419716939937510

class SignalProcessor:
    def __init__(self, num_points=64):
        """
        初始化信号处理器
        Initialize signal processor
        
        Args:
            num_points: FFT点数，必须是2的幂次（32, 64, 128, 256等）
            FFT points, must be power of 2 (32, 64, 128, 256, etc.)
            
        重要参数说明 | Important Parameters:
        - num_points: 决定频率分辨率和计算复杂度
        - 点数越多，频率分辨率越高，但计算量越大
        """
        self.num_points = num_points
        self.data = []  # 存储时域信号数据
    
    def generate_test_signal(self):
        """
        生成测试信号 - 包含5个不同频率的余弦波叠加
        Generate test signal - sum of 5 cosine waves with different frequencies
        
        信号构成 | Signal Composition:
        - 5个不同频率和幅值的余弦波叠加
        - 用于验证FFT能够正确识别各个频率成分
        - 实际应用中可替换为真实的传感器数据
        """
        self.data = []  # 清空数据
        for i in range(self.num_points):
            # 生成5个不同频率、不同幅值的余弦波
            # Generate 5 cosine waves with different frequencies and amplitudes
            
            # 基础频率成分 - 1倍频
            data0 = 10 * math.cos(2 * PI * i / self.num_points)      # 幅值10，基波
            
            # 二次谐波 - 2倍频  
            data1 = 20 * math.cos(2 * 2 * PI * i / self.num_points)  # 幅值20，二次谐波
            
            # 三次谐波 - 3倍频
            data2 = 30 * math.cos(3 * 2 * PI * i / self.num_points)  # 幅值30，三次谐波
            
            # 高频小信号 - 4倍频
            data3 = 0.2 * math.cos(4 * 2 * PI * i / self.num_points) # 幅值0.2，高频小信号
            
            # 强高频信号 - 5倍频
            data4 = 1000 * math.cos(5 * 2 * PI * i / self.num_points)# 幅值1000，强高频信号
            
            # 将所有波形叠加，生成复合信号
            # Sum all waves together to create composite signal
            composite_signal = data0 + data1 + data2 + data3 + data4
            
            # 转换为整数并存储（模拟ADC采样）
            # Convert to integer (simulating ADC sampling)
            self.data.append(int(composite_signal))
        
        print(f"生成测试信号完成，包含 {len(self.data)} 个采样点")
        print(f"信号幅值范围: {min(self.data)} 到 {max(self.data)}")
        return self.data
    
    def perform_fft(self, sampling_rate=38400):
        """
        执行FFT变换
        Perform FFT analysis
        
        Args:
            sampling_rate: 采样率(Hz) / Sampling rate in Hz
                        决定频率分析的范围和精度
            
        返回 | Returns:
            dict: 包含FFT结果、幅值谱和频率点的字典
        
        FFT处理流程 | FFT Processing Flow:
        1. 数据准备 -> 2. FFT计算 -> 3. 频谱计算 -> 4. 频率映射
        """
        try:
            print(f"\n开始FFT分析，点数: {self.num_points}, 采样率: {sampling_rate}Hz")
            
            # 将列表转换为numpy数组，指定数据类型为16位无符号整数
            # Convert list to numpy array with 16-bit unsigned integer type
            # 模拟实际ADC采样的数据格式
            data_array = np.array(self.data, dtype=np.uint16)
            print("数据数组转换完成")
            
            # 创建FFT对象并执行变换
            # Create FFT object and perform transform
            # 参数说明：
            # - data_array: 输入时域信号
            # - self.num_points: FFT点数
            # - 0x555: 配置参数（具体含义参考硬件手册）
            fft_obj = FFT(data_array, self.num_points, 0x555)
            print("FFT对象创建成功")
            
            # 获取FFT结果（复数形式，包含实部和虚部）
            # Get FFT results (complex form, contains real and imaginary parts)
            fft_result = fft_obj.run()
            print("FFT计算完成")
            
            # 计算幅值谱 - 将复数结果转换为幅度值
            # Calculate amplitude spectrum - convert complex results to magnitude values
            # 幅值计算公式: magnitude = sqrt(real^2 + imag^2)
            amplitude_spectrum = fft_obj.amplitude(fft_result)
            print("幅值谱计算完成")
            
            # 计算频率点 - 将FFT结果索引映射到实际频率值
            # Calculate frequency points - map FFT result indices to actual frequencies
            # 频率分辨率 = 采样率 / FFT点数
            frequency_points = fft_obj.freq(self.num_points, sampling_rate)
            print("频率点计算完成")
            
            return {
                'fft_result': fft_result,        # 原始FFT复数结果
                'amplitude': amplitude_spectrum, # 幅值谱（用于分析信号强度）
                'frequencies': frequency_points  # 对应的频率值（Hz）
            }
            
        except Exception as e:
            print(f"FFT计算错误 / FFT calculation error: {e}")
            print("可能的原因 | Possible reasons:")
            print("  - 内存不足 | Insufficient memory")
            print("  - 点数不是2的幂 | Points not power of 2")
            print("  - 硬件FFT模块故障 | Hardware FFT module failure")
            return None

def main():
    """
    主函数 - 演示完整的FFT分析流程
    Main function - demonstrates complete FFT analysis workflow
    """
    print("=== FFT频域分析演示程序 ===")
    print("=== FFT Frequency Domain Analysis Demo ===")
    
    # 创建信号处理器实例，使用64点FFT
    # Create signal processor instance with 64-point FFT
    processor = SignalProcessor(64)
    
    # 生成测试信号（包含多个频率成分的复合信号）
    # Generate test signal (composite signal with multiple frequency components)
    print("\n1. 生成测试信号...")
    signal = processor.generate_test_signal()
    print("原始信号前10个点 / First 10 points of original signal:", signal[:10])
    
    # 执行FFT分析，使用38.4kHz采样率
    # Perform FFT analysis with 38.4kHz sampling rate
    print("\n2. 执行FFT分析...")
    results = processor.perform_fft(sampling_rate=38400)
    
    if results:
        print("\n3. FFT分析结果:")
        print("   ====================")
        
        # 显示FFT原始结果（复数）
        print("\n   FFT原始结果 (前5个点):")
        for i in range(min(5, len(results['fft_result']))):
            print(f"     点{i}: {results['fft_result'][i]}")
        
        # 显示幅值谱（最重要的分析结果）
        print(f"\n   幅值谱 (所有{len(results['amplitude'])}个点):")
        print("   ", results['amplitude'])
        
        # 显示频率点映射
        print(f"\n   频率点映射 (Hz):")
        print("   ", results['frequencies'])
        
        # 分析主要频率成分
        print("\n4. 主要频率成分分析:")
        print("   ====================")
        amplitudes = results['amplitude']
        frequencies = results['frequencies']
        
        # 找出幅值最大的几个频率成分（忽略直流分量）
        significant_indices = sorted(range(1, len(amplitudes)), 
                                   key=lambda i: amplitudes[i], 
                                   reverse=True)[:5]
        
        for idx in significant_indices:
            if amplitudes[idx] > 0.1:  # 只显示显著的频率成分
                print(f"   频率: {frequencies[idx]:.1f}Hz, 幅值: {amplitudes[idx]:.2f}")
    
    else:
        print("\nFFT分析失败，请检查硬件和参数设置")

if __name__ == "__main__":
    main()

"""
=== FFT技术详解 ===

1. 频率分辨率：
   频率分辨率 = 采样率 / FFT点数
   本例中：38400Hz / 64点 = 600Hz
   即每个频率点代表600Hz的频率范围

2. 奈奎斯特频率：
   最高可分析频率 = 采样率 / 2 = 19200Hz
   FFT结果的后半部分是前半部分的镜像

3. 幅值谱解释：
   - 索引0: 直流分量（信号的平均值）
   - 索引1~N/2-1: 正频率成分
   - 索引N/2~N-1: 负频率成分（通常忽略）

4. 实际应用场景：
   - 音频频谱分析
   - 振动故障诊断
   - 电源质量分析
   - 通信信号处理

=== 预期分析结果 ===
在幅值谱中应该能明显看到5个峰值，对应生成的5个测试频率成分，
且幅值大小应与生成信号时的设置成比例。
"""
复制代码

代码解读：
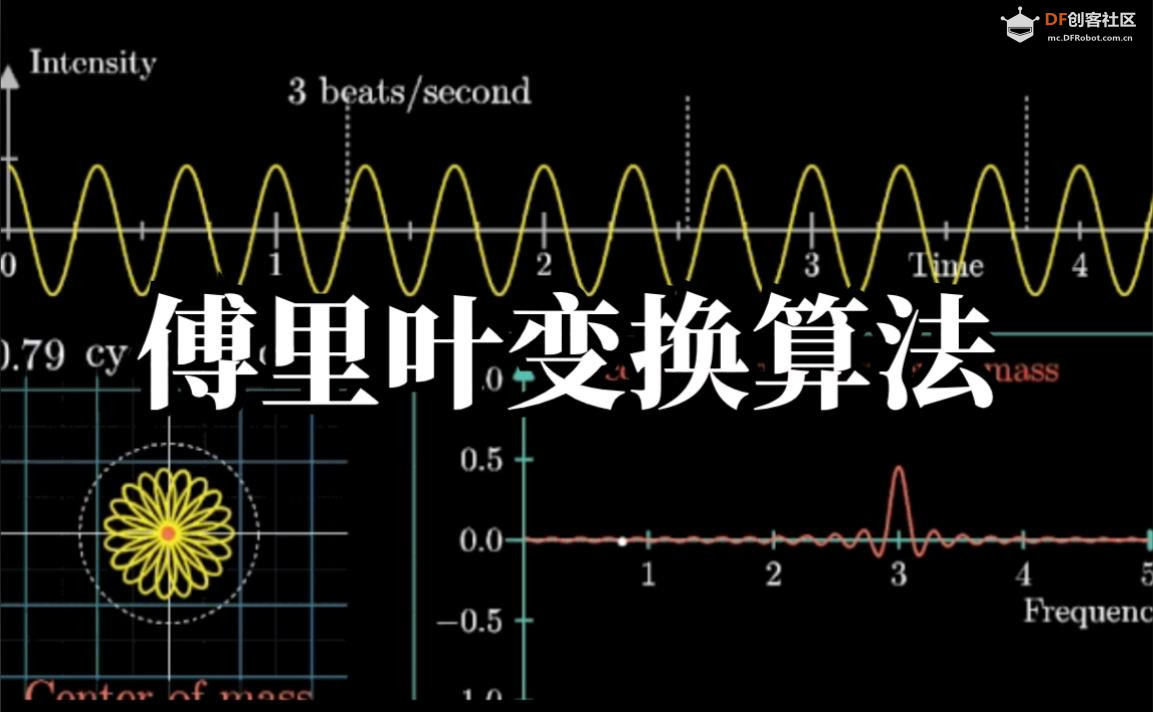
FFT点数选择：必须是2的幂次，平衡分辨率与计算量
采样率设定：根据信号最高频率成分，满足奈奎斯特采样定理
频率分辨率：Δf = 采样率 / FFT点数，决定区分相近频率的能力
幅值谱分析：识别信号中的主要频率成分及其强度
硬件优势：K230的硬件FFT大幅提升计算效率，适合实时处理

这个示例展示了从信号生成到频域分析的完整流程，是数字信号处理的基础应用。


实验串口返回情况